【题目】如图,将一个长方形放置在平面直角坐标系中,![]() ,点
,点![]() 是
是![]() 的中点,反比例函数图像过点
的中点,反比例函数图像过点![]() 且和
且和![]() 相交于点
相交于点![]() .
.
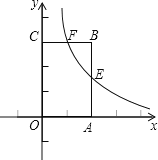
(1)求直线![]() 和反比例函数的解析式;
和反比例函数的解析式;
(2)求四边形![]() 的面积.
的面积.
参考答案:
【答案】(1)直线OB的解析式是y=![]() x.反比例函数的解析式是y=
x.反比例函数的解析式是y=![]() ;(2)3.
;(2)3.
【解析】
(1)根据OA=2,OC=3,得到点B的坐标,再进一步运用待定系数法求直线OB的解析式,根据E是AB的中点,求得点E的坐标,再进一步运用待定系数法求得反比例函数的解析式;
(2)根据反比例函数的解析式求得点F的横坐标,再进一步根据四边形的面积等于矩形的面积减去两个直角三角形的面积进行计算.
(1)由题意得B(2,3),E(2,![]() ),
),
设直线OB的解析式是y=k1x,
把B点坐标代入,得k1=![]() ,
,
则直线OB的解析式是y=![]() x.
x.
设反比例函数解析式是y=![]() ,
,
把E点坐标代入,得k2=3,
则反比例函数的解析式是y=![]() ;
;
(2)由题意得Fy=3,代入y=![]() ,
,
得Fx=1,即F(1,3).
则四边形OEBF的面积=矩形OABC的面积-△OAE的面积-△OCF的面积=6-3=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,DC∥AB,∠A=90°,AB=26cm,DC=18cm ,AD=4cm,动点M以1cm/s的速度从点D向点C运动,动点N从点B以2cm/s的速度向点A运动点M、N同时出发,当其中一个动点到达端点时停止运动,另一个动点也随之停止运动,设动点运动时间为t(s),四边形ANMD的面积y(
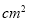 ),y关于x的函数解析式并写出定义域_____.
),y关于x的函数解析式并写出定义域_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张骑自行车匀速从甲地到乙地,在途中休息了-段时间后,仍按原速行驶他距乙地的距离与时间的关系如图中折线所示,小李骑摩托车匀速从乙地到甲地,比小张晚出发一段时间,他距乙地的距离与时间的关系如图中线段AB所示,
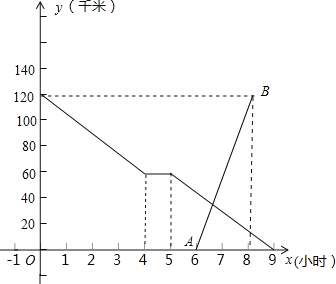
(1)小李到达甲地后,再经过 小时小张到达乙地;小张骑自行车的速度是 千米/小时;
(2)请你写出小李距乙地的距离y(千米)与时间x(小时)之间的函数关系(不要求写出定义域);
(3)若小李想在小张休息期间(第4小时和第5小时不算小张休息)与他相遇,则他出发的时间x应在什么范围?(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的周长是20 cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为68 cm2,那么矩形ABCD的面积是_______cm2.

-
科目: 来源: 题型:
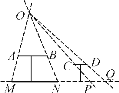
查看答案和解析>>【题目】如图,AB是公园的一圆桌的主视图,MN表示该桌面在路灯下的影子,CD则表示一个圆形的凳子.
(1)请在图中标出路灯O的位置,并画出CD的影子PQ;
(2)若桌面直径与桌面距地面的距离为1.2 m,测得影子的最大跨度MN为2 m,求路灯O与地面的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完.该公司的年产量为6000件,若在国内市场销售,平均每件产品的利润与国内销售量
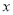 的关系如下表:
的关系如下表:销售量
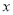 (千件)
(千件)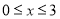
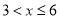
单件利润(元)
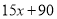
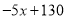
若在国外销售,平均每件产品的利润与国外的销售数量
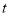 的关系如下表:
的关系如下表:销售量
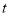 (千件)
(千件)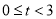
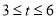
单件利润(元)
100
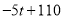
(1)用
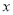 的代数式表示
的代数式表示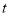 为:
为: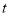 =;
=;(2)该公司每年国内、国外的销售量各为多少时,可使公司每年的总利润为60万元?
相关试题

