【题目】(1)如图,两个圈分别表示负数集和分数集. 请你把下列各数填入表示它所在的数集的圈里:
-50% , 2011 , 0.618 , -3 ,![]() ,0 , 5.9,-3.14 , -92 .
,0 , 5.9,-3.14 , -92 .

(2)图中,这两个圈的重叠部分表示什么数的集合?
(3)在(1)的数据中,求最大的数与最小的数之和.
参考答案:
【答案】(1)根据题意如图:
(2)这两个圈的重叠部分表示负分数集合;
(3)最大的数与最小的数之和1919.
【解析】
(1)根据有理数的分类对题目进行分类即可得到答案;
(2)根据负分数的定义即可得出答案;
(3)先找出这组数据中的最大数和最小数,再把这两个数进行相加即可得出答案.
(1)根据题意如图:
(2)这两个圈的重叠部分表示负分数集合;
(3)∵最大数是2011,最小数是92,
∴最大的数与最小的数之和201192=1919.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D为BC边的中点,以D为顶点的∠EDF的两边分别与AB、AC交于点E、F,且∠EDF与∠A互补.
(1)如图①,若AB=AC,且∠A=90°,证明:DE=DF;
(2)如图②,若AB=AC,那么(1)中的结论是否成立?请说明理由.
(3)如图③,若
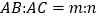 ,探索线段DE与DF的数量关系,并证明你的结论.
,探索线段DE与DF的数量关系,并证明你的结论.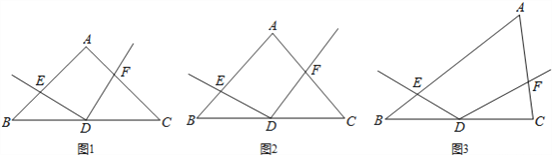
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.求∠DCE的大小.
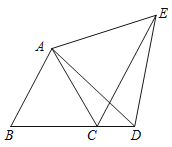
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把按一定规律排列的一列数称为数列,若对于一个数列中任意相邻有序的三个数
 ,
,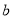 ,
, ,总满足
,总满足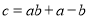 ,则称这个数列为理想数列.
,则称这个数列为理想数列.(1)在数列①
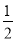 ,
,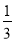 ,
,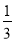 ,
,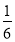 ;②3,-2,-1,1中,是理想数列的是______(只填序号即可)
;②3,-2,-1,1中,是理想数列的是______(只填序号即可)(2)如果数列
 ,是理想数列,求
,是理想数列,求 的值;
的值;(3)若数列
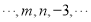 ,是理想数列,求代数式
,是理想数列,求代数式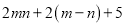 的值;
的值;(4)请写出一个由五个不同正整数组成的理想数列:______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解并解答:
为了求1+2+22+23+24+…+22009的值,可令S=1+2+22+23+24+…+22009,
则2S=2+22+23+24+…+22009+22010,因此2S﹣S=(2+22+23+…+22009+22010)﹣(1+2+22+23+…+22009)=22010﹣1.
所以:S=22010﹣1.即1+2+22+23+24+…+22009=22010﹣1.
请依照此法,求:1+4+42+43+44+…+42010的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于
 MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
-
科目: 来源: 题型:
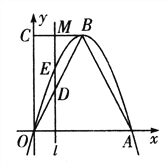
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线
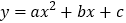 与
与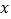 轴交于O点、A点,B为抛物线上一点,C为y轴上一点,连接BC,且BC//OA,已知点O(0,0),A(6,0),B(3,m),AB=
轴交于O点、A点,B为抛物线上一点,C为y轴上一点,连接BC,且BC//OA,已知点O(0,0),A(6,0),B(3,m),AB= .
.(1)求B点坐标及抛物线的解析式.,
(2)M是CB上一点,过点M作y轴的平行线交抛物线于点E,求DE的最大值;
(3)坐标平面内是否存在一点F,使得以C、B、D、F为顶点的四边形是菱形?若存在,求出符合条件的点F坐标;若不存在,请说明理由.

相关试题

