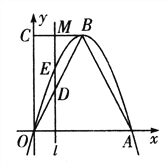
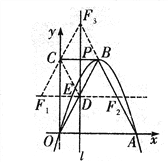
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于O点、A点,B为抛物线上一点,C为y轴上一点,连接BC,且BC//OA,已知点O(0,0),A(6,0),B(3,m),AB=
轴交于O点、A点,B为抛物线上一点,C为y轴上一点,连接BC,且BC//OA,已知点O(0,0),A(6,0),B(3,m),AB=![]() .
.
(1)求B点坐标及抛物线的解析式.,
(2)M是CB上一点,过点M作y轴的平行线交抛物线于点E,求DE的最大值;
(3)坐标平面内是否存在一点F,使得以C、B、D、F为顶点的四边形是菱形?若存在,求出符合条件的点F坐标;若不存在,请说明理由.

参考答案:
【答案】(1)B(6,0),y=![]() ;(2)
;(2)![]() ;(3) 满足条件的F点共3个:
;(3) 满足条件的F点共3个:![]() ,
,![]() ,
,![]()
【解析】分析:(1)运用勾股定理求出m的值,根据题意得点B为抛物线的顶点,设设抛物线为![]() ,即可求解;
,即可求解;
(2)可求![]() ,设E
,设E![]() ,则D(
,则D(![]() ,故DE=
,故DE=![]() ,从而可得结果;
,从而可得结果;
(3)设F![]() ,根据菱形的判定分三种情况进行讨论计算即可得解.
,根据菱形的判定分三种情况进行讨论计算即可得解.
详解:(1)如图,过点B作BG⊥OA于G,

由A(6,0),O(0,0)知抛物线对称轴为直线![]() ,
,
∴点B为抛物线的顶点。
∴AG=OG=3,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
∴B(3,6),
设抛物线为![]() ,过点B(6,0),
,过点B(6,0),
∴9a+6=0
∴a=-![]() ,
,
∴y=-![]() (x-3)2+6=-
(x-3)2+6=-![]() x2+4x;
x2+4x;
(2)可求![]() ,设E
,设E![]() ,则D(
,则D(![]() ,
,
∴DE=![]() ,
,
∴当x=![]() ,DE最大=
,DE最大=![]() .
.
(3)设F![]() ,
,
![]()
①当CD为菱形对角线时,
∵FD∥BC,
∴![]()
∴
解得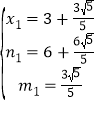 (舍去),
(舍去),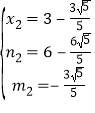 .
.
②当BD为菱形对角线时,![]()
∴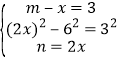
∴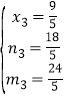 ,
,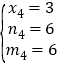 (舍去)
(舍去)
![]()
③当BC为菱形对角线时,D、F均在BC的垂直平分线上,且FP=PD,
则![]() ,则D(
,则D(![]() ,则PD=3,则
,则PD=3,则![]() ,
,![]() ,
,![]() 。
。
综上所述,满足条件的F点共3个:![]() ,
,![]() ,
,![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,两个圈分别表示负数集和分数集. 请你把下列各数填入表示它所在的数集的圈里:
-50% , 2011 , 0.618 , -3 ,
 ,0 , 5.9,-3.14 , -92 .
,0 , 5.9,-3.14 , -92 .
(2)图中,这两个圈的重叠部分表示什么数的集合?
(3)在(1)的数据中,求最大的数与最小的数之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解并解答:
为了求1+2+22+23+24+…+22009的值,可令S=1+2+22+23+24+…+22009,
则2S=2+22+23+24+…+22009+22010,因此2S﹣S=(2+22+23+…+22009+22010)﹣(1+2+22+23+…+22009)=22010﹣1.
所以:S=22010﹣1.即1+2+22+23+24+…+22009=22010﹣1.
请依照此法,求:1+4+42+43+44+…+42010的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于
 MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直接写出结果
(1)﹣7﹣3=
(2)2.5-(-3.5)=
(3)
 -1=
-1= (4)
 ÷(﹣2)=
÷(﹣2)=(5)﹣(﹣5)2=
(6)|+7|﹣|﹣5|=
(7)- 3xy-4xy ﹦
(8)3x-2
 +3
+3 ﹦
﹦(9)
 +
+ ﹦
﹦ (10)6
 -5
-5 ﹦
﹦ -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,△ABC中,∠C=90°,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形(不写作法,但须保留作图痕迹).
(2)已知内角度数的两个三角形如图2,图3所示.请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点
 (n为正整数)都在数轴上,点
(n为正整数)都在数轴上,点 在原点O的左边,且
在原点O的左边,且 ;点
;点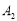 在原点O的右边,且
在原点O的右边,且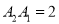 ;点
;点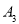 在原点O的左边,且
在原点O的左边,且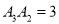 ;点
;点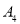 在 原点O的右边,且
在 原点O的右边,且 ;….依照上述规律,点
;….依照上述规律,点 ,
, 所表示的数分别为( )
所表示的数分别为( )A.1008,-1008B.1008,-1009
C.2016,-2017D.-2016,2017
相关试题

