Question

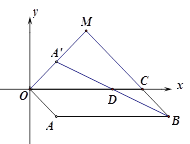
【题目】在平面直角坐标系xOy中，点C坐标为（6，0），以原点O为顶点的四边形OABC是平行四边形，将边OA沿x轴翻折得到线段，连接交线段OC于点D.

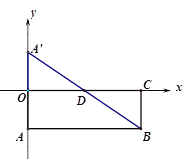
（1）如图1，当点A在y轴上，且A（0，-2）时.

① 求所在直线的函数表达式；

② 求证：点D为线段的中点．

（2）如图2，当时， ，BC的延长线相交于点M，试探究的值，并写出探究思路．

Answer 1

【答案】(1)① ,②见解析;(2)

【解析】试题分析：（1）① 先求点A、B的坐标，再根据对称求得的坐标，再用待定系数法求直线B的解析式；②根据ASA证明△≌△BDC，再得出=BD，即点D是的中点；（2）连接交x轴于F点，先证明F为的中点，得出点D为线段的中点，由边OA沿x轴翻折得到线段且 ，得出， ，又由AO∥BC得出，过点D作DE∥BM交OM于点E ，可得，所以，再得到． .

试题解析：

（1）①四边形OABC是平行四边形

∴AO∥BC，AO=BC ．

又∵点A落在y轴上，

∴AO⊥x轴，

∴BC⊥x轴．

∵A（0，-2）C（6，0），

∴B（6，-2）．

又∵边OA沿x轴翻折得到线段，

∴（0，2）．

设直线的函数表达式为 ，

解得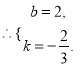

∴所在直线的函数表达式为．

证明：②∵四边形OABC是平行四边形，

∴AO∥BC，AO=BC ．

∴∠=∠DBC．

又∵边OA沿x轴翻折得到线段，

∴AO= ．

∴=BC．

又∵∠=∠BDC，

∴△≌△BDC

∴=BD，

∴点D为线段的中点．

（2）

理由：连接交x轴于F点

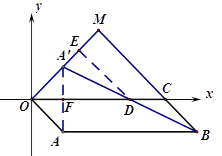
证明F为的中点；

∴ 得出点D为线段的中点

∵边OA沿x轴翻折得到线段且 ，

∴， ．

∵AO∥BC，

∴．

过点D作DE∥BM交OM于点E ，

可得，

还可得到等腰直角△．

∴．

∴．