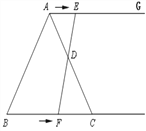
【题目】如图,在等边三角形ABC中,BC=6cm. 射线AG//BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s) ;
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)求当t为何值时,四边形ACFE是菱形;
(3)是否存在某一时刻t,使以A、F、C、E为顶点的四边形内角出现直角?若存在,求出t的值;若不存在,请说明理由.
参考答案:
【答案】(1)证明见解析; (2)t=6; (3)存在,理由见解析.
【解析】分析:(1)由题意得到AD=CD,再由AG与BC平行,利用两直线平行内错角相等得到两对角相等,利用AAS即可得证;(2)若四边形ACFE是菱形,则有CF=AC=AE=6,由E的速度求出E运动的时间即可;(3)分两种情况考虑:若CE⊥AG,此时四点构成三角形,不是直角梯形;若AF⊥BC,求出BF的长度及时间t的值.
本题解析:(1) 证明:∵AG∥BC ,∴![]() ,∵
,∵![]() 是AC边的,∴AD=CD
是AC边的,∴AD=CD
又∵![]() , ∴△ADE≌△CDF
, ∴△ADE≌△CDF
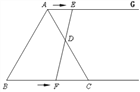
(2)∵当四边形ACFE是菱形时,∴AE=AC=CF=EF,
由题意可知:AE=t,CF=2T-6,∴t=6,
(3)当四边形内角有直角时,分两种情况:若四边形ACFE是直角梯形,此时EF⊥AG, 过![]() 作CM⊥AG于M,AM=3可以得到AE-CF=AM,
作CM⊥AG于M,AM=3可以得到AE-CF=AM,
即t-(2t-6)=3,∴t=3,
此时,C与F重合,不符合题意,舍去。
若四边形![]() 是直角梯形,此时AF⊥BC,
是直角梯形,此时AF⊥BC,
∵△ABC是等边三角形,F是BC中点,
∴2t=3,经检验,符合题意,∴t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的每个内角都等于144°,求它的边数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个四边形截去一个角后,它不可能是( )
A.六边形
B.五边形
C.四边形
D.三角形 -
科目: 来源: 题型:
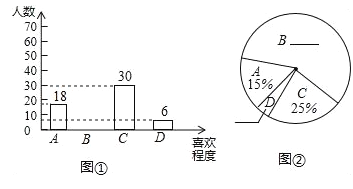
查看答案和解析>>【题目】(本题满分5分)某校为了七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有学生中,每班随机抽取6名学生,并对他们的数学学习情况进行了问卷调查,我们从调查的题目中特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A—非常喜欢”、“B—比较喜欢”、“C—不太喜欢”、“D—很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项而且只能选一项)结果进行统计。现将统计结果制成如下两幅不完整的统计图。请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取的学生对于数学学习喜欢程度的众数是:
(3)若该校七年级有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的两边长分别是2和7,另一边长a为偶数,且2<a<8,则这个三角形的周长为
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式x2-6x+9分解因式,结果正确的是( )
A.(x-3)2
B.(x-9)2
C.(x+3)(x-3)
D.(x+9)(x-9) -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:
(1)3a2﹣3b2
(2)2x2﹣12x+18.
相关试题

