【题目】如图,直线y=![]() x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数表达式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,求点P的坐标;
②若△PQB的面积为![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.

参考答案:
【答案】(1)y=﹣![]() x+3;(2)①P(﹣
x+3;(2)①P(﹣![]() ,0);②M(
,0);②M(![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).
【解析】
(1)先根据坐标轴上点的特点求出A,B的坐标,进而求出点C坐标,最后用待定系数法即可得出结论;
(2)①设出点M的坐标,利用勾股定理求出BC2=45,BM2=OM2+OB2=m2+9,MC2=(6﹣m)2,最后用勾股定理建立方程求解,即可得出结论;
②设出点M的坐标,进而得出点P,Q坐标,即:得出PQ,最后用面积公式即可得出结论.
解:(1)对于y=![]() x+3,令x=0,y=3,
x+3,令x=0,y=3,
∴B(0,3),
令y=0,
∴![]() x+3=0,
x+3=0,
∴x=﹣6,
∴A(﹣6,0),
∵点C与点A关于y轴对称,
∴C(6,0),
设直线BC的解析式为y=kx+b,
∴![]() ,
,
∴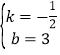 ,
,
∴直线BC的解析式为y=﹣![]() x+3;
x+3;
(2)①设点M(m,0),
∴P(m,![]() m+3),
m+3),
∵B(0,3),C(6,0),
∴BC2=45,BM2=OM2+OB2=m2+9,MC2=(6﹣m)2,
∵∠MBC=90°,
∴△BMC是直角三角形,
∴BM2+BC2=MC2,
∴m2+9+45=(6﹣m)2,
∴m=﹣![]() ,∴P(﹣
,∴P(﹣![]() ,0);
,0);
②设点M(n,0),
∵点P在直线AB:y=![]() x+3上,
x+3上,
∴P(n,![]() n+3),
n+3),
∵点Q在直线BC:y=﹣![]() x+3上,
x+3上,
∴Q(n,﹣![]() n+3),
n+3),
∴PQ=|![]() n+3﹣(﹣
n+3﹣(﹣![]() n+3)|=|n|,
n+3)|=|n|,
∵△PQB的面积为![]() ,
,
∴S△PQB=![]() |n||n|=
|n||n|=![]() n2=
n2=![]() ,
,
∴n=±![]() ,
,
∴M(![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在 Rt△ABC中,∠ABC=90°, BD平分∠ ABC,∠CAD=45, AC=4,点E是线段BD的中点,则CE的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合,研究数轴我们发现:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为
 .如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为
.如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为 =3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
=3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).(1)用含t的代数式表示:t秒后,点P表示的数为 ,点Q表示的数为 .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=
 AB;
AB;(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】感恩是中华民族的传统美德,在4月份某校提出了“感恩父母、感恩老师、感恩他人”的“三感”教育活动.感恩事例有:A.给父母过一次生日;B .为父母做一次家务活,让父母休息一天;C.给老师一个发自内心的拥抱,并且与老师谈心;D.帮助有困难的同学度过难关.为了解学生对这四种感恩事例的情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学在4种感恩事例中选择最想做的一种),将数据进行整理并绘制成以下两幅统计图(未画完整).

(1)这次调查中,一共查了名学生;
(2)请补全扇形统计图中的数据及条形统计图;
(3)若有3名选 A的学生,1名选 C的学生组成志愿服务队外出参加联谊活动,欲从中随机选出2人担任活动负责人,请通过树状图或列表求两人均是选 A的学生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一长、宽、高分别是 5cm,4cm,3cm 的长方体木块,一只蚂蚁要从长方体的一个顶点 A处沿长方体的表面爬到长方体上和 A 相对的顶点 B 处,则需要爬行的最短路径长为( )

A. 5
 cmB.
cmB.  cmC. 4
cmC. 4 cmD. 3
cmD. 3 cm
cm -
科目: 来源: 题型:
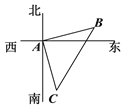
查看答案和解析>>【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1
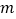 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BCA=90°,CD 是边 AB上的中线,分别过点 C , D 作 BA , BC的平行线交于点 E ,且 DE 交 AC 于点 O ,连接 AE .

(1)求证:四边形 ADCE 是菱形;
(2)若AC=2DE,求 sin∠CDB的值.
相关试题

