【题目】如图,△ABC中,∠BCA=90°,CD 是边 AB上的中线,分别过点 C , D 作 BA , BC的平行线交于点 E ,且 DE 交 AC 于点 O ,连接 AE .
(1)求证:四边形 ADCE 是菱形;
(2)若AC=2DE,求 sin∠CDB的值.
参考答案:
【答案】
(1)证明:∵DE∥BC,CE∥AB,
∴四边形DBCE是平行四边形,
∴EC=BD,
又∵CD是AB边上的中线,
∴AD=BD,
∴EC=AD ,
又∵EC∥AD,
∴四边形ADCE是平行四边形,
∵∠BCA=90°,CD是斜边AB上的中线,
∴AD=CD,
∴四边形ADCE是菱形.
(2)解:如下图:
过点C作CF⊥AB于点F,
由(1)得,BC=DE,
设BC=x,则AC=2x,
在Rt![]() ABC中,AB=
ABC中,AB=![]() =
=![]() x,
x,
∵![]() AB
AB![]() CF=
CF=![]() AC
AC![]() BC,
BC,
∴CF=![]() =
=![]() x,
x,
∵CD=![]() AB=
AB=![]() x,
x,
∴sin∠CDB=![]() =
=![]() .
.
【解析】本题考查菱形的判定与性质,平行四边形的判定与性质以及勾股定理、锐角三角函数的定义等,依照题意准确作出辅助线是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.(1)求直线BC的函数表达式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,求点P的坐标;
②若△PQB的面积为
 ,请直接写出点M的坐标.
,请直接写出点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一长、宽、高分别是 5cm,4cm,3cm 的长方体木块,一只蚂蚁要从长方体的一个顶点 A处沿长方体的表面爬到长方体上和 A 相对的顶点 B 处,则需要爬行的最短路径长为( )

A. 5
 cmB.
cmB.  cmC. 4
cmC. 4 cmD. 3
cmD. 3 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1
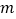 ).
).
-
科目: 来源: 题型:
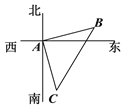
查看答案和解析>>【题目】如图,有一艘货船和一艘客船同时从港口A出发,客船每小时比货船多走5海里,客船与货船速度的比为4:3,货船沿东偏南10°方向航行,2小时后货船到达B处,客船到达C处,若此时两船相距50海里.
(1)求两船的速度分别是多少?
(2)求客船航行的方向.
-
科目: 来源: 题型:
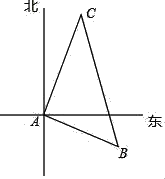
查看答案和解析>>【题目】现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若AC=b,BC=a,请你利用这个图形解决下列问题:
(1)试说明a2+b2=c2;
(2)如果大正方形的面积是6,小正方形的面积是2,求(a+b)2的值.
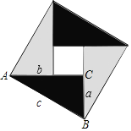
-
科目: 来源: 题型:
查看答案和解析>>【题目】福田区某轿车销售公司为龙泉工业区代销 A 款轿车,为了吸引购车族,销售公司打出降价牌,今年 5月份A款轿车每辆售价比去年同期每辆售价低 1万元,如果卖出相同数量的 A 款轿车,去年的销售额为100万元,今年销售额只有90万元.
(1)今年 5月份 A 款轿车每辆售价为多少元?
(2)为了增加收入,该轿车公司决定再为龙泉工业区代销 B款轿车,已知 A款轿车每辆进价为 7.5万元,B款轿车每辆进价为 6万元,公司预计用不多于105万元的资金购进这两款轿车共 15 辆,但A款轿车不多于6辆,试问共有几种进货方案?
(3)在⑵的条件下,B款轿车每辆售价为 8万元,为打开B款轿车的销路,公司决定每售出一辆 B款轿车,返还顾客现金a( 0<a ≤1 )万元.假设购进的15辆车能够全部卖出去,试讨论采用哪种进货方案可以使该轿车销售公司卖出这 15辆车后获得最大利润?
相关试题

