【题目】如图1,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线y=![]() x2﹣
x2﹣![]() x+3的绳子.
x+3的绳子.
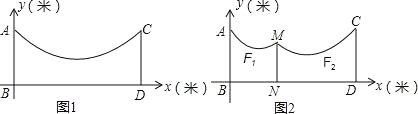
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为![]() ,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
参考答案:
【答案】(1)![]() m;(2)MN的长度为2.1m;(3)m的取值范围是4≤m≤8﹣2
m;(2)MN的长度为2.1m;(3)m的取值范围是4≤m≤8﹣2![]() .
.
【解析】
试题分析:(1)直接利用配方法求出二次函数最值得出答案;(2)利用顶点式求出抛物线F1的解析式,进而得出x=3时,y的值,进而得出MN的长;(3)根据题意得出抛物线F2的解析式,得出k的值,进而得出m的取值范围.
试题解析:(1)∵a=![]() >0,
>0,
∴抛物线顶点为最低点,
∵y=![]() x2﹣
x2﹣![]() x+3=
x+3=![]() (x﹣4)2+
(x﹣4)2+![]() ,
,
∴绳子最低点离地面的距离为:![]() m;
m;
(2)由(1)可知,对称轴为x=4,则BD=8,
令x=0得y=3,
∴A(0,3),C(8,3),
由题意可得:抛物线F1的顶点坐标为:(2,1.8),
设F1的解析式为:y=a(x﹣2)2+1.8,
将(0,3)代入得:4a+1.8=3,
解得:a=0.3,
∴抛物线F1为:y=0.3(x﹣2)2+1.8,
当x=3时,y=0.3×1+1.8=2.1,
∴MN的长度为:2.1m;
(3)∵MN=DC=3,
∴根据抛物线的对称性可知抛物线F2的顶点在ND的垂直平分线上,
∴抛物线F2的顶点坐标为:(![]() m+4,k),
m+4,k),
∴抛物线F2的解析式为:y=![]() (x﹣
(x﹣![]() m﹣4)2+k,
m﹣4)2+k,
把C(8,3)代入得:![]() (8﹣
(8﹣![]() m﹣4)2+k=3,
m﹣4)2+k=3,
解得:k=﹣![]() (4﹣
(4﹣![]() m)2+3,
m)2+3,
∴k=﹣![]() (m﹣8)2+3,
(m﹣8)2+3,
∴k是关于m的二次函数,
又∵由已知m<8,在对称轴的左侧,
∴k随m的增大而增大,
∴当k=2时,﹣![]() (m﹣8)2+3=2,
(m﹣8)2+3=2,
解得:m1=4,m2=12(不符合题意,舍去),
当k=2.5时,﹣![]() (m﹣8)2+3=2.5,
(m﹣8)2+3=2.5,
解得:m1=8﹣2![]() ,m2=8+2
,m2=8+2![]() (不符合题意,舍去),
(不符合题意,舍去),
∴m的取值范围是:4≤m≤8﹣2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三元一次方程组
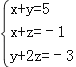 .
.
(1)求该方程组的解;
(2)若该方程组的解使ax+2y+z<0成立,求整数a的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,点A(1,﹣2)关于原点对称的点的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于( )
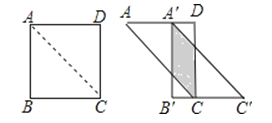
A.4
B.6或4
C.8
D.4或8 -
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)我市某校在推进新课改的过程中,开设的体育选修课有:A:篮球,B:足球,C:排球,D:羽毛球,E:乒乓球,学生可根据自己的爱好选修一门,学校李老师对某班全班学生的选课情况进行调查统计,制成了两幅不完整的统计图(如图).
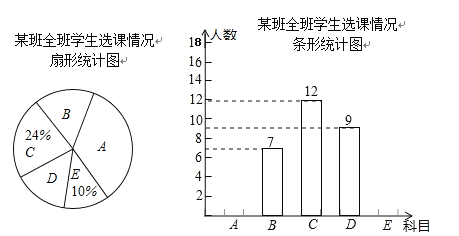
(1)请你求出该班的总人数,并补全频数分布直方图;
(2)表示“足球”所在扇形的圆心角是多少度?
(3)该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣2x﹣8与x轴的交点坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,求AB和CD之间的距离.
相关试题

