搜索
【题目】抛物线y=x2﹣2x﹣8与x轴的交点坐标是 ．
参考答案：
【答案】（4，0）（﹣2，0）
【解析】解：令y=0，则x2﹣2x﹣8=0．
（x﹣4）（x+2）=0
解得x=4或x=﹣2．
则抛物线y=x2﹣2x﹣8与x轴的交点坐标是（4，0），（﹣2，0）．
所以答案是：（4，0），（﹣2，0）．
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识，掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将边长为12的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△A′B′C′，当两个三角形重叠部分的面积为32时，它移动的距离AA′等于（ ）
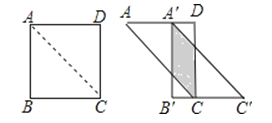
A.4
B.6或4
C.8
D.4或8 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，地面BD上两根等长立柱AB，CD之间悬挂一根近似成抛物线y=
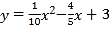x2﹣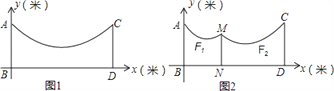
x+3的绳子．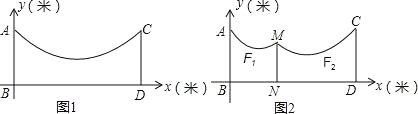
（1）求绳子最低点离地面的距离；
（2）因实际需要，在离AB为3米的位置处用一根立柱MN撑起绳子（如图2），使左边抛物线F1的最低点距MN为1米，离地面1.8米，求MN的长；
（3）将立柱MN的长度提升为3米，通过调整MN的位置，使抛物线F2对应函数的二次项系数始终为
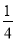，设MN离AB的距离为m，抛物线F2的顶点离地面距离为k，当2≤k≤2.5时，求m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】（7分）我市某校在推进新课改的过程中，开设的体育选修课有：A：篮球，B：足球，C：排球，D：羽毛球，E：乒乓球，学生可根据自己的爱好选修一门，学校李老师对某班全班学生的选课情况进行调查统计，制成了两幅不完整的统计图（如图）．
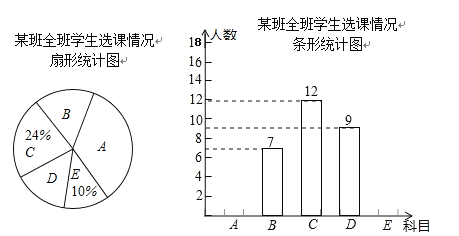
（1）请你求出该班的总人数，并补全频数分布直方图；
（2）表示“足球”所在扇形的圆心角是多少度？
（3）该班班委4人中，1人选修篮球，2人选修足球，1人选修排球，李老师要从这4人中人选2人了解他们对体育选修课的看法，请你用列表或画树状图的方法，求选出的2人恰好1人选修篮球，1人选修足球的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本题满分8分）已知⊙O的半径为13cm，弦AB∥CD，AB＝24cm，CD＝10cm，求AB和CD之间的距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若x＝0是关于x的一元二次方程（m+2）x2﹣3x+m2﹣4＝0的一个根，则m的值为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线与x轴交于A（－1，0），B（3，0），与y轴交于C（0，－3），顶点为点M．
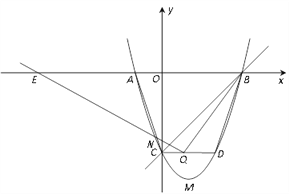
（1）求抛物线的解析式及点M的坐标．
（2）点P是直线BC在y轴右侧部分图象上的动点，若点P，点C，点M所构成的三角形与△AOC相似，求符合条件的P点坐标．
（3）过点C作CD∥AB，CD交抛物线于点D，点Q是线段CD上的一动点，作直线QN与线段AC交于点N，与x轴交于点E，且∠BQE＝∠BDC，当CN的值最大时，求点E的坐标．
相关试题
