【题目】已知三元一次方程组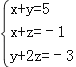 .
.
(1)求该方程组的解;
(2)若该方程组的解使ax+2y+z<0成立,求整数a的最大值.
参考答案:
【答案】【解答】解: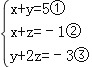
①﹣②得:y﹣z=6④,
③与④组成二元一次方程组![]() ,
,
解得:![]() ;
;
把y=3代入①,解得x=2,
所以三元一次方程组的解为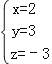 ;
;
(2)∵该方程组的解使ax+2y+z<0成立,
∴2a+6﹣3<0,
∴a<![]() ,
,
∴整数a的最大值为﹣2.
【解析】(1)根据解三元一次方程组的步骤先消去一个未知数,得到一个二元一次方程组,从而得出答案;
(2)将(1)中所求的方程组的解代入ax+2y+z<0,求出a的取值范围,进而得到整数a的最大值.
【考点精析】通过灵活运用二元一次方程的解,掌握适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,底角x为(单位:度),顶角y(单位:度)
(1)写出y与x的函数解析式
(2)求自变量x的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】①对顶角相等;②两点之间线段最短;③相等的角是对顶角;④同位角相等.其中假命题有( )
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,点A(1,﹣2)关于原点对称的点的坐标是 .
-
科目: 来源: 题型:
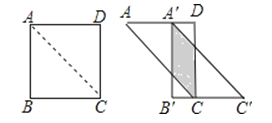
查看答案和解析>>【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于( )
A.4
B.6或4
C.8
D.4或8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线y=
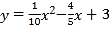 x2﹣
x2﹣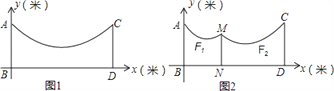 x+3的绳子.
x+3的绳子.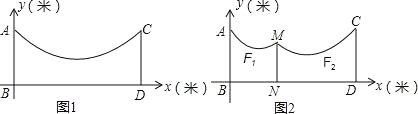
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为
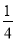 ,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
相关试题

