【题目】我市某风景区门票价格如图所示,百姓旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
(1)求W关于x的函数关系式,并写出自变量x 的取值范围;
(2)若甲团队人数不超过100人,请说明甲、乙两团队联合购票比分别购票最多可节约多少元.
参考答案:
【答案】
(1)
解:∵甲团队人数为x人,乙团队人数不超过50人,
∴120﹣x≤50,解得:x≥70.
①当70≤x≤100时,W=70x+80(120﹣x)=﹣10x+9600;
②当100<x<120时,W=60x+80(120﹣x)=﹣20x+9600.
综上所述,W= ![]()
(2)
解:∵甲团队人数不超过100人,
∴x≤100,W=﹣10x+9600,
∵70≤x≤100,W随x的增大而减少,
∴x=70时,W取最大值,最大值=﹣10×70+9600=8900(元),
若两团联合购票需120×60=7200(元),
∴最多可节约8900﹣7200=1700(元).
答:甲、乙两团队联合购票比分别购票最多可节约1700元钱.
【解析】(1)由甲团队人数为x人,乙团队人数不超过50人,可得出关于x的一元一次不等式,解不等式可得出x的取值范围,结合门票价与人数的关系分段考虑,由总钱数=甲团队购票钱数+乙团队购票钱数得出函数关系式;(2)由甲团队人数不超过100人,选定所用W关于x的函数解析式,由一次函数的单调性结合x的取值范围可得出W的最大值,用其减去甲乙团队合作购票所需钱数即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△ABD中,AD与BC相交于O点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC=BD,并给出证明.
你添加的条件是?并证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】电视节目“奔跑吧兄弟”播出后深受中小学生的喜爱,小刚想知道大家最喜欢哪位“兄弟”,于是在本校随机抽取了一部分学生进行抽查(每人只能选一个自己最喜欢的“兄弟”),将调查结果进行了整理后绘制成如图两幅不完整的统计图,请结合图中提供的信息解答下列问题:

(1)本次被调查的学生有多少人.
(2)将两幅统计图补充完整.
(3)若小刚所在学校有2000名学生,请根据图中信息,估计全校喜欢“Angelababy”的人数.
(4)若从3名喜欢“李晨”的学生和2名喜欢“Angelababy”的学生中随机抽取两人参加文体活动,则两人都是喜欢“李晨”的学生的概率是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π.
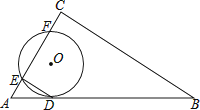
(1)求证:DE∥BC;
(2)若AF=CE,求线段BC的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:
说明:
方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点
纸片利用率= ×100%
×100%
发现:

(1)方案一中的点A、B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.
探究:
(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.
说明:方案三中的每条边均过其中两个正方形的顶点. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.

(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,∠A=30°.分别以顶点A、B为圆心,大于
 AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.下列结论中,错误的是( )
AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.下列结论中,错误的是( )
A.直线AB是线段MN的垂直平分线
B.CD= AD
AD
C.BD平分∠ABC
D.S△APD=S△BCD
相关试题

