Question

【题目】操作：小明准备制作棱长为1cm的正方体纸盒，现选用一些废弃的纸片进行如下设计：
说明：
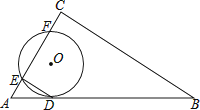
方案一：图形中的圆过点A、B、C；
方案二：直角三角形的两直角边与展开图左下角的正方形边重合，斜边经过两个正方形的顶点
纸片利用率= ×100%
发现：

（1）方案一中的点A、B恰好为该圆一直径的两个端点．你认为小明的这个发现是否正确，请说明理由．
（2）小明通过计算，发现方案一中纸片的利用率仅约为38.2%．请帮忙计算方案二的利用率，并写出求解过程．
探究：
（3）小明感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直接写出方案三的利用率．
说明：方案三中的每条边均过其中两个正方形的顶点．

Answer 1

【答案】
（1）

解：发现：小明的这个发现正确．

理由：

解法一：如图一：连接AC、BC、AB，

∵AC=BC=，AB=2

∴AC2+BC2=AB2，

∴∠BCA=90°，

∴AB为该圆的直径．

解法二：如图二

：连接AC、BC、AB．

易证△AMC≌△BNC，

∴∠ACM=∠CBN．

又∵∠BCN+∠CBN=90°，

∴∠BCN+∠ACM=90°，

即∠BCA=90°，

∴AB为该圆的直径．

（2）

解：如图三：

∵DE=FH，DE∥FH，

∴∠AED=∠EFH，

∵∠ADE=∠EHF=90°，

∴△ADE≌△EHF（ASA），

∴AD=EH=1．

∵DE∥BC，

∴△ADE∽△ACB，

∴ ，

∴ ，

∴BC=8，

∴S△ACB=16．

∴该方案纸片利用率= ×100%= ×100%=37.5%；

（3）

解：

探究：过点C作CD⊥EF于D，过点G作GH∥AC，交BC于点H，

设AP=a，

∵PQ∥EK，

易得△APQ∽△KQE，△CEF是等腰三角形，△GHL是等腰三角形，

∴AP：AQ=QK：EK=1：2，

∴AQ=2a，PQ= a，

∴EQ=5a，

∵EC：ED=QE：QK，

∴EC= a，

则PG=5a+ a= a，GL= a，

∴GH= a，

∵ ，

解得：GB= a，

∴AB= a，AC= a，

∴S△ABC= span> ×AB×AC= a2，

S展开图面积=6×5a2=30a2，

∴该方案纸片利用率= ×100%= ×100%=49.86%．

【解析】（1）连接AC、BC、AB，由AC=BC= ，AB= ，根据勾股定理的逆定理，即可求得∠BAC=90°，又由90°的圆周角所对的弦是直径，则可证得AB为该圆的直径；（2）首先证得△ADE≌△EHF与△ADE∽△ACB，即可求得AD与BC的长，求得△ABC的面积，即可求得该方案纸片利用率；（3）利用方案（2）的方法，分析求解即可求得答案．
【考点精析】根据题目的已知条件，利用几何体的展开图和勾股定理的概念的相关知识可以得到问题的答案，需要掌握沿多面体的棱将多面体剪开成平面图形，若干个平面图形也可以围成一个多面体；同一个多面体沿不同的棱剪开，得到的平面展开图是不一样的，就是说：同一个立体图形可以有多种不同的展开图；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．