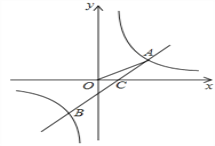
【题目】如图,反比例函数y=![]() 与反比例函数y=k2
与反比例函数y=k2![]() +b的图象的交点为A(m,1)、B(-2,n),OA与
+b的图象的交点为A(m,1)、B(-2,n),OA与![]() 轴正方向的夹角为α,且tanα=
轴正方向的夹角为α,且tanα=![]() 。
。
(1)求反比例函数及一次函数的表达式;
(2)设直线AB与x轴交于点C,且AC与x轴正方向的夹角为β,求tanβ的值。
参考答案:
【答案】(1)直线AB的解析式为y=![]() x-1;(2)
x-1;(2)![]() .
.
【解析】试题分析:(1)用待定系数法求函数表达式,需要知道图像上点的坐标,根据![]() ,构造直角三角形OAE,把三角函数值转化为边的比,可求出A点横坐标,把A坐标代入
,构造直角三角形OAE,把三角函数值转化为边的比,可求出A点横坐标,把A坐标代入![]() ,求得反比例函数解析式
,求得反比例函数解析式![]() ,把B坐标代入求出n=-2,把A、B坐标代入y=k2x+b即可求出一次函数解析式
,把B坐标代入求出n=-2,把A、B坐标代入y=k2x+b即可求出一次函数解析式![]() ;(2)易求C坐标(2,0),在Rt△ACE中,AE=1,CE=2,可求出tanβ的值.
;(2)易求C坐标(2,0),在Rt△ACE中,AE=1,CE=2,可求出tanβ的值.
试题解析:(1)过A作AE⊥x轴于E,∵tan∠AOE=tanα=![]() ,∴OE=4AE.又∵A(m,1),∴AE=1,AE=4,∴点A(4,1).∵A点在反比例函数
,∴OE=4AE.又∵A(m,1),∴AE=1,AE=4,∴点A(4,1).∵A点在反比例函数![]() 图像上,∴k1=4,∴反比例函数为
图像上,∴k1=4,∴反比例函数为![]() .∵B(-2,n)在反比例函数
.∵B(-2,n)在反比例函数![]() 图像上,∴n="-2." ∴B的坐标是(-2,-2), 将A,B两点的坐标代入直线y=k2x+b得:
图像上,∴n="-2." ∴B的坐标是(-2,-2), 将A,B两点的坐标代入直线y=k2x+b得: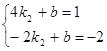 ,解得k2=
,解得k2=![]() ,b="-1," ∴直线AB的解析式为y=
,b="-1," ∴直线AB的解析式为y=![]() x-1;
x-1;
(2)∵直线AB的表达式为y=![]() x-1,令y=0,得x="2," ∴C(2,0), 又∵A(4,1),∴CE=2,AE=1.
x-1,令y=0,得x="2," ∴C(2,0), 又∵A(4,1),∴CE=2,AE=1.
∴tanβ=![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠B+∠BCD=180°,∠B=∠D.

求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD ( )
∴∠B=_______( )
又∵∠B=∠D(已知 ),
∴∠D=_______( )
∴AD∥BE( )
∴∠E=∠DFE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个全等的小长方形,再按图2围成一个较大的正方形.

(1)图2中的阴影部分的正方形的边长可表示为________;
(2)请用两种不同的方法表示图2中阴影部分的面积: 方法1:________;
方法2:________;
(3)观察图2,请你写出下列三个代数式之间的等量关系: 代数式:(m+n)2 , (m﹣n)2 , mn.________;
(4)根据(3)题中的等量关系,解决问题: 若m+n=5,mn=4,求m﹣n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠1+∠2=90°,∠1+∠3=90°,那么∠2与∠3的大小关系是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值大于1而不大于3的所有整数的和是 。
-
科目: 来源: 题型:
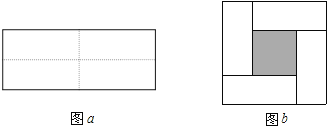
查看答案和解析>>【题目】图a是一个长为2m,宽为2n的长方形,沿图a中虚线用剪刀把它均分成四块小长方形,然后按图b的形状拼成一个正方形.
(1)请用两种不同的方法求图b中阴影部分的面积:
方法1: ____ (只列式,不化简)
方法2: ______ (只列式,不化简)
(2)观察图b,写出代数式(m+n)2,(m-n)2,mn之间的等量关系: ______ ;
(3)根据(2)题中的等量关系,解决如下问题:若a+b=7,ab=5,则(a-b)2= ______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计,请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:


频率分布表 频数分布直方图
(1)这次抽取了名学生的竞赛成绩进行统计,其中:
 ,
,  ;
;(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
相关试题

