【题目】计算
(1)(![]() )﹣2﹣(﹣2)0+(﹣0.2)2018×(﹣5)2018;
)﹣2﹣(﹣2)0+(﹣0.2)2018×(﹣5)2018;
(2)用整式乘法公式计算:1012﹣1;
(3)(x2y+2x2y﹣y3)÷y﹣(y+2x)(2x﹣y);
(4)先化简,再求值:(a﹣2b)2+(a﹣b)(a+b)﹣2(a﹣3b)(a﹣b),其中,a=1,b=﹣2.
参考答案:
【答案】(1)4;(2)10200;(3)﹣x2;(4)4ab﹣3b2,﹣20.
【解析】
(1)根据负指数幂的运算公式与幂的运算即可求解;
(2)根据平方差公式即可计算;
(3)根据整式的运算法则即可化简;
(4)根据完全平方公式及整式的运算法则即可求解.
(1)原式=4﹣1+[(﹣0.2)×(﹣5)]2018
=4﹣1+1
=4;
(2)原式=(101+1)×(101﹣1)
=102×100
=10200;
(3)原式=x2+2x2﹣y2﹣(4x2﹣y2)
=3x2﹣y2﹣4x2+y2
=﹣x2;
(4)原式=a2﹣4ab+4b2+a2﹣b2﹣2(a2﹣ab﹣3ab+3b2)
=a2﹣4ab+4b2+a2﹣b2﹣2a2+2ab+6ab﹣6b2
=4ab﹣3b2.
当a=1,b=﹣2时,
原式=4×1×(﹣2)﹣3×(﹣2)2
=﹣8﹣12
=﹣20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y1=
 的图象与函数y2=kx+b的图象交于点A(﹣1,a)B(﹣8+a,1)
的图象与函数y2=kx+b的图象交于点A(﹣1,a)B(﹣8+a,1)
(1)求函数y=
 和y=kx+b的表达式;
和y=kx+b的表达式;(2)观察图象,直接写出不等式
 <kx+b的解.
<kx+b的解. -
科目: 来源: 题型:
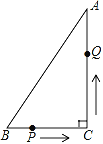
查看答案和解析>>【题目】如图,在Rt△ABC中,AC=24cm,BC=7cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.
(1)当t为何值时,P、Q两点的距离为5
 cm?
cm?(2)当t为何值时,△PCQ的面积为15cm2?
(3)请用配方法说明,点P运动多少时间时,四边形BPQA的面积最小?最小面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两公司为“见义勇为基金会”各捐款3000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐20元.请你根据上述信息,就这两个公司的“人数”或“人均捐款”提出一个用分式方程解决的题,并写出解题过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A、E、F、C在一条直线上,BE∥DF,BE=DF,AF=CE.
(1)图中有几对全等三角形?
(2)判断AD与BC的位置关系,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题:

(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?
(2)已知洗衣机的排水速度为每分钟19升.
①求排水时洗衣机中的水量y(升)与时间x(分钟)与之间的关系式;
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于90万元.已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润为1950万元?

相关试题

