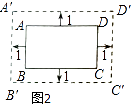
【题目】将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是 ( ) 
A.新三角形与原三角形相似
B.新矩形与原矩形相似
C.新三角形与原三角形、新矩形与原矩形都相似
D.都不相似
参考答案:
【答案】A
【解析】解:根据题意得:AB∥A′B′,AC∥A′C′,BC∥B′C′,
∴∠A=∠A′,∠B=∠B′,
∴△ABC∽△A′B′C′;
∵根据题意得:AB=CD=3,AD=BC=5,则A′B′=C′D′=3+2=5,A′D′=B′C′=5+2=7,
∴ ![]() ,
, ![]() ,
,
∴新矩形与原矩形对应边的比不相等,
∴新矩形与原矩形不相似,
故选:A
【考点精析】通过灵活运用相似图形,掌握形状相同,大小不一定相同(放大或缩小);判定:①平行;②两角相等;③两边对应成比例,夹角相等;④三边对应成比例即可以解答此题.
-
科目: 来源: 题型:
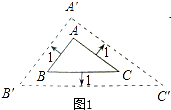
查看答案和解析>>【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=
 ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
①李明同学做了如图乙的辅助线,将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′,从而问题得到解决.你能说明其中理由并完成问题解答吗?
②如图丙,在正方形ABCD内有一点P,且PA=
 ,BP=
,BP= ,PC=1;求∠BPC度数的大小和正方形ABCD的边长.
,PC=1;求∠BPC度数的大小和正方形ABCD的边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
(1)a=40,m=1;
(2)乙的速度是80km/h;
(3)甲比乙迟
 h到达B地;
h到达B地;(4)乙车行驶
 小时或
小时或 小时,两车恰好相距50km.
小时,两车恰好相距50km.正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
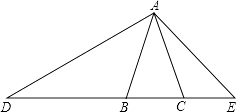
查看答案和解析>>【题目】如图,在△ABC中,已知AB=AC,D、E、B、C在同一条直线上,且AB2=BDCE,求证:△ABD∽△ECA.
-
科目: 来源: 题型:
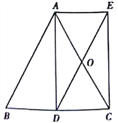
查看答案和解析>>【题目】如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E
使AE∥BC,连接AE。
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积= ;
②若AB=10,则BC= 时,四边形ADCE是正方形。
-
科目: 来源: 题型:
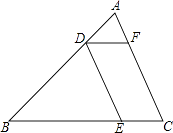
查看答案和解析>>【题目】如图,在△ABC中,点D是边AB的四等分点,DE∥AC,DF∥BC,AC=8,BC=12,求四边形DECF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB,P1是AB的黄金分割点(AP1>BP1),点O是AB的中点,P2是P1关于点O的对称点.求证:P1B是P2B和P1P2的比例中项.
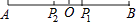
相关试题

