【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
(1)a=40,m=1;
(2)乙的速度是80km/h;
(3)甲比乙迟![]() h到达B地;
h到达B地;
(4)乙车行驶![]() 小时或
小时或![]() 小时,两车恰好相距50km.
小时,两车恰好相距50km.
正确的个数是( )

A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】C
【解析】(1)由题意,得m=1.5﹣0.5=1.
120÷(3.5﹣0.5)=40(km/h),则a=40,故(1)正确;
(2)120÷(3.5﹣2)=80km/h(千米/小时),故(2)正确;
(3)设甲车休息之后行驶路程y(km)与时间x(h)的函数关系式为y=kx+b,由题意,得
![]()
解得: ![]()
∴y=40x﹣20,
根据图形得知:甲、乙两车中先到达B地的是乙车,
把y=260代入y=40x﹣20得,x=7,
∵乙车的行驶速度:80km/h,
∴乙车的行驶260km需要260÷80=3.25h,
∴7﹣(2+3.25)=![]() h,
h,
∴甲比乙迟![]() h到达B地,故(3)正确;
h到达B地,故(3)正确;
(4)当1.5<x≤7时,y=40x﹣20.
设乙车行驶的路程y与时间x之间的解析式为y=k'x+b',由题意得
![]()
解得: ![]()
∴y=80x﹣160.
当40x﹣20﹣50=80x﹣160时,
解得:x=![]() .
.
当40x﹣20+50=80x﹣160时,
解得:x=![]() .
.
∴![]() ﹣2=
﹣2=![]() ,
, ![]() ﹣2=
﹣2=![]() .
.
所以乙车行驶小时![]() 或
或![]() 小时,两车恰好相距50km,故(4)错误.
小时,两车恰好相距50km,故(4)错误.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,D、E是AB、AC上点,AB=7.8,AD=3,AC=6,AE=3.9,试判断△ADE与△ABC是否会相似.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,…….照此规律,点P第100次跳动至点P100的坐标是( )

A. (-26,50) B. (-25,50) C. (26,50) D. (25,50)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=
 ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
①李明同学做了如图乙的辅助线,将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′,从而问题得到解决.你能说明其中理由并完成问题解答吗?
②如图丙,在正方形ABCD内有一点P,且PA=
 ,BP=
,BP= ,PC=1;求∠BPC度数的大小和正方形ABCD的边长.
,PC=1;求∠BPC度数的大小和正方形ABCD的边长. -
科目: 来源: 题型:
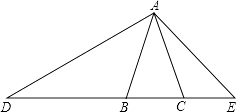
查看答案和解析>>【题目】如图,在△ABC中,已知AB=AC,D、E、B、C在同一条直线上,且AB2=BDCE,求证:△ABD∽△ECA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是 ( )

A.新三角形与原三角形相似
B.新矩形与原矩形相似
C.新三角形与原三角形、新矩形与原矩形都相似
D.都不相似 -
科目: 来源: 题型:
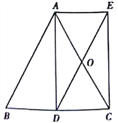
查看答案和解析>>【题目】如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E
使AE∥BC,连接AE。
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积= ;
②若AB=10,则BC= 时,四边形ADCE是正方形。
相关试题

