【题目】如图,已知线段AB,P1是AB的黄金分割点(AP1>BP1),点O是AB的中点,P2是P1关于点O的对称点.求证:P1B是P2B和P1P2的比例中项. ![]()
参考答案:
【答案】证明:设AB=2,
∵P1是AB的黄金分割点(AP1>BP1),
∴AP1= ![]() ×2=
×2= ![]() ﹣1,
﹣1,
∴P1B=2﹣( ![]() ﹣1)=3﹣
﹣1)=3﹣ ![]() ,
,
∵点O是AB的中点,
∴OB=1,
∴OP1=1﹣(3﹣ ![]() )=
)= ![]() ﹣2,
﹣2,
∵P2是P1关于点O的对称点,
∴P1P2=2( ![]() ﹣2)=2
﹣2)=2 ![]() ﹣4,
﹣4,
∴P2B=2 ![]() ﹣4+3﹣
﹣4+3﹣ ![]() =
= ![]() ﹣1,
﹣1,
∵P1B2=(3﹣ ![]() )2=14﹣6
)2=14﹣6 ![]() ,P2BP1P2=(
,P2BP1P2=( ![]() ﹣1)(2
﹣1)(2 ![]() ﹣4)=14﹣6
﹣4)=14﹣6 ![]() ,
,
∴P1B2=P2BP1P2,
∴P1B是P2B和P1P2的比例中项
【解析】设AB=2,根据黄金分割的定义得AP1= ![]() AB=
AB= ![]() ﹣1,则P1B=3﹣
﹣1,则P1B=3﹣ ![]() ,由点O是AB的中点得OB=1,所以OP1=
,由点O是AB的中点得OB=1,所以OP1= ![]() ﹣2,由于P2是P1关于点O的对称点,则P1P2=2
﹣2,由于P2是P1关于点O的对称点,则P1P2=2 ![]() ﹣4,可计算出P2B=
﹣4,可计算出P2B= ![]() ﹣1,然后同过计算得到P1B2=14﹣6
﹣1,然后同过计算得到P1B2=14﹣6 ![]() ,P2BP1P2=14﹣6
,P2BP1P2=14﹣6 ![]() ,即P1B2=P2BP1P2,所以P1B是P2B和P1P2的比例中项.
,即P1B2=P2BP1P2,所以P1B是P2B和P1P2的比例中项.
【考点精析】掌握黄金分割是解答本题的根本,需要知道把线段AB分成两条线段AC,BC(AC>BC),并且使AC是AB和BC的比例中项,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=0.618AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是 ( )

A.新三角形与原三角形相似
B.新矩形与原矩形相似
C.新三角形与原三角形、新矩形与原矩形都相似
D.都不相似 -
科目: 来源: 题型:
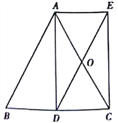
查看答案和解析>>【题目】如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E
使AE∥BC,连接AE。
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积= ;
②若AB=10,则BC= 时,四边形ADCE是正方形。
-
科目: 来源: 题型:
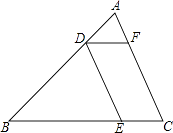
查看答案和解析>>【题目】如图,在△ABC中,点D是边AB的四等分点,DE∥AC,DF∥BC,AC=8,BC=12,求四边形DECF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点.

-
科目: 来源: 题型:
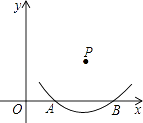
查看答案和解析>>【题目】如图,在直角坐标系中,以点P为圆心的圆弧与x轴交于A,B两点,已知P(4,2)和A(2,0),则点B的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中,且A
 、B
、B 、C
、C .将其平移后得到
.将其平移后得到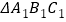 ,若A,B的对应点是
,若A,B的对应点是 ,
, ,C的对应点
,C的对应点 的坐标是
的坐标是 .
.(1)在平面直角坐标系中画出△ABC;
(2)写出点
 的坐标是_____________,
的坐标是_____________, 坐标是___________;
坐标是___________;(3)此次平移也可看作
 向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
相关试题

