【题目】如图l,在四边形ABCD中.∠DAB被对角线AC平分,且AC2=AB·AD,我们称该四边形为“可分四边形”∠DAB称为“可分角”.

(1)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,求证:△DAC∽△CAB.
(2)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB 则∠DAB = .
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4.BC=2.∠D=90°,则AD= .
参考答案:
【答案】(1)见详解;(2)120°;(3)![]()
【解析】
(1)先判断出![]() ,即可得出结论;
,即可得出结论;
(2)由已知条件可证得△ADC∽△ACB,得出D=∠4,再由已知条件和三角形内角和定理得出∠1+2∠1=180°,求出∠1=60°,即可得出∠DAB的度数;
(3)由已知得出AC2=ABAD,∠DAC=∠CAB,证出△ADC∽△ACB,得出∠D=∠ACB=90°,由勾股定理求出AB,即可得出AD的长.
解:(1)证明:∵四边形ABCD为“可分四边形”,∠DAB为“可分角”,
∴AC2=ABAD,
∴![]() ,
,
∵∠DAB为“可分角”,
∴∠CAD=∠BAC,
∴△DAC∽△CAB;
(2)解:如图所示:

∵AC平分∠DAB,
∴∠1=∠2,
∵AC2=ABAD,
∴AD:AC=AC:AB,
∴△ADC∽△ACB,
∴∠D=∠4,
∵∠DCB=∠DAB,
∴∠DCB=∠3+∠4=2∠1,
∵∠1+∠D+∠3=∠1+∠4+∠3=180°,
∴∠1+2∠1=180°,
解得:∠1=60°,
∴∠DAB=120°;
故答案为:120;
(3)解:∵四边形ABCD为“可分四边形”,∠DAB为“可分角”,
∴AC2=ABAD,∠DAC=∠CAB,
∴AD:AC=AC:AB,
∴△ADC∽△ACB,
∴∠D=∠ACB=90°,
∴![]() ,
,
∴![]()
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市304国道通辽至霍林郭勒段在修建过程中经过一座山峰,如图所示,其中山脚A、C两地海拔高度约为1000米,山顶B处的海拔高度约为1400米,由B处望山脚A处的俯角为30°,由B处望山脚C处的俯角为45°,若在A、C两地间打通一隧道,求隧道最短为多少米(结果取整数,参考数据
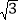 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
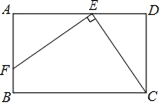
查看答案和解析>>【题目】如图,点E、F分别在矩形ABCD的两条边上,且EF⊥EC,EF=EC,若该矩形的周长为16,AE=3,则DE的长为( )
A.
 B. 2 C.
B. 2 C.  D. 3
D. 3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一四柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示,根据图象提供的信息,解答下列问题:
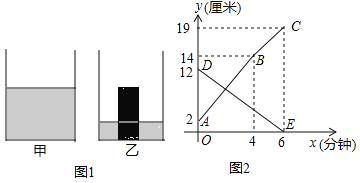
(1)图2中折线ABC表示 槽中水的深度与注水时间关系,线段DE表示 槽中水的深度与注水时间之间的关系(以上两空选填“甲”或“乙”),点B的纵坐标表示的实际意义是 .
(2)注水多长时间时,甲、乙.两个水槽中水的深度相同?
(3)若乙槽底面积为36平方厘米(壁厚不计),则乙槽中铁块的体积为 立方厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有
 、
、 、
、 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )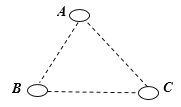
A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
-
科目: 来源: 题型:
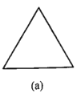
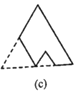
查看答案和解析>>【题目】如图所示,图(a)是一块边长为1,周长记为
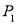 的正三角形纸板,沿图(a)的底边剪去一块边长为
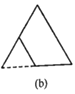
的正三角形纸板,沿图(a)的底边剪去一块边长为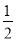 的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
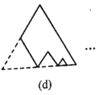
的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的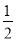 后,得图(c),(d),……,记第
后,得图(c),(d),……,记第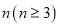 )块纸板的周长为Pn.则
)块纸板的周长为Pn.则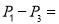 ____;
____;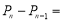 _______.
_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于给定的一次函数y=ax+b(a≠0),把形如
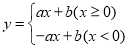 的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).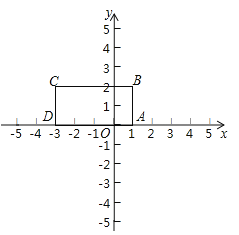
(1)已知函数y=2x+l.
①若点P(-1,m)在这个一次函数的衍生函数图像上,则m= .
②这个一次函数的衍生函数图像与矩形ABCD的边的交点坐标分别为 .
(2)当函数y=kx-3(k>0)的衍生函数的图象与矩形ABCD有2个交点时,k的取值范围是 .
相关试题

