【题目】探究与发现:
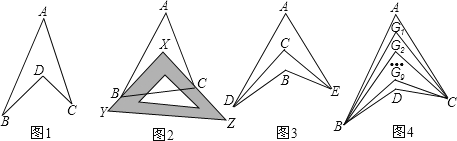
如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX= °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠BG1C=77°,求∠A的度数.
参考答案:
【答案】(1)∠BDC=∠A+∠B+∠C,理由见解析;(2)①40°;②90°;③70°.
【解析】
(1)根据题意观察图形连接AD并延长至点F,根据一个三角形的外角等于与它不相邻的两个内角的和可证∠BDC=∠BDF+∠CDF;
(2)①由(1)的结论可得∠ABX+∠ACX+∠A=∠BXC,然后把∠A=50°,∠BXC=90°代入上式即可得到∠ABX+∠ACX的值;
②结合图形可得∠DBE=∠DAE+∠ADB+∠AEB,代入∠DAE=50°,∠DBE=130°即可得到∠ADB+∠AEB的值,再利用上面得出的结论可知∠DCE=![]() (∠ADB+∠AEB)+∠A,易得答案.
(∠ADB+∠AEB)+∠A,易得答案.
③由②方法,进而可得答案.
解:(1)连接AD并延长至点F,

由外角定理可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD;
∵∠BDC=∠BDF+∠CDF,
∴∠BDC=∠BAD+∠B+∠C+∠CAD.
∵∠BAC=∠BAD+∠CAD;
∴∠BDC=∠BAC +∠B+∠C;
(2)①由(1)的结论易得:∠ABX+∠ACX+∠A=∠BXC,
又因为∠A=50°,∠BXC=90°,
所以∠ABX+∠ACX=90°﹣50°=40°;
②由(1)的结论易得∠DBE=∠DAE +∠ADB+∠AEB,
∵∠DAE=50°,∠DBE=130°,
∴∠ADB+∠AEB=80°;
∴∠DCE=![]() (ADB+∠AEB)+A=40°+50°=90°;
(ADB+∠AEB)+A=40°+50°=90°;
③由②知,∠BG1C=![]() (ABD+∠ACD)+A,
(ABD+∠ACD)+A,
∵∠BG1C=77°,
∴设∠A为x°,
∵∠ABD+∠ACD=140°﹣x°,
∴![]() (40﹣x)x=77,
(40﹣x)x=77,
∴14﹣![]() x+x=77,
x+x=77,
∴x=70,
∴∠A为70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 的表达式为
的表达式为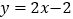 ,直线
,直线 与x轴交于点D,直线
与x轴交于点D,直线 :
: 与x轴交于点A,且经过点B,直线
与x轴交于点A,且经过点B,直线 、
、 交于点
交于点 .
.(1)求m的值;
(2)求直线
 的表达式;
的表达式;(3)根据图象,直接写出
 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2开始,连续的偶数相加,它们和的情况如下表:

(1)若n=7时,则S的值为___.
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=___.
根据上题的规律计算:300+302+304+…+2016+2018+2020的值.
-
科目: 来源: 题型:
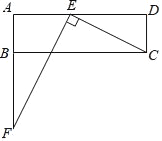
查看答案和解析>>【题目】如图,在矩形ABCD中,已知 AD>AB.在边AD上取点E,连结CE.过点E作EF⊥CE,与边AB的延长线交于点F.
(1)证明:△AEF∽△DCE.
(2)若AB=4,AE=6,AD=14,求线段AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,
 ),则点C的坐标为( )
),则点C的坐标为( )
A. (
 ,-1)B. (-1,
,-1)B. (-1, )C. (
)C. ( ,1)D. (-
,1)D. (- ,1)
,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,
 ,AD平分∠CAB,交CB于点D,过点D作
,AD平分∠CAB,交CB于点D,过点D作 于点E.若
于点E.若 ,CD=5,.
,CD=5,.(1)求BD的长
(2)AE与BE相等吗?说明理由。
(3)求△ABC的面积

-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”黄金周,坚胜家电城大力促销,收银情况一直看好
 下表为当天与前一天的营业额的涨跌情况
下表为当天与前一天的营业额的涨跌情况 已知9月30日的营业额为26万元.
已知9月30日的营业额为26万元.10月1日
2日
3日
4日
5日
6日
7日
4
3
2
0
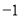


 黄金周内收入最低的哪一天?
黄金周内收入最低的哪一天? 直接回答,不必写过程
直接回答,不必写过程 .
. 黄金周内平均每天的营业额是多少?
黄金周内平均每天的营业额是多少?
相关试题

