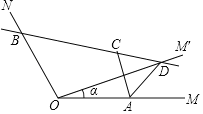
【题目】如图,已知∠MON=120°,点A,B分别在OM,ON上,且OA=OB=a,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(0°<α<120°且α≠60°),作点A关于直线OM′的对称点C,画直线BC交OM′于点D,连接AC,AD,有下列结论:
①AD=CD;
②∠ACD的大小随着α的变化而变化;
③当α=30°时,四边形OADC为菱形;
④△ACD面积的最大值为![]() a2;
a2;
其中正确的是_____.(把你认为正确结论的序号都填上).
参考答案:
【答案】①③④
【解析】①根据对称的性质:对称点的连线被对称轴垂直平分可得:OM'是AC的垂直平分线,再由垂直平分线的性质可作判断;
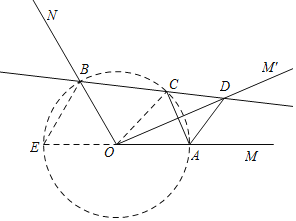
②以O为圆心,以OA为半径作⊙O,交AO的延长线于E,连接BE,则A、B、C都在⊙O上,根据四点共圆的性质得:∠ACD=∠E=60°,说明∠ACD是定值,不会随着α的变化而变化;
③当α=30°时,即∠AOD=∠COD=30°,证明△AOC是等边三角形和△ACD是等边三角形,得OC=OA=AD=CD,可作判断;
④先证明△ACD是等边三角形,当AC最大时,△ACD的面积最大,当AC为直径时最大,根据面积公式计算后可作判断.
①∵A、C关于直线OM'对称,
∴OM'是AC的垂直平分线,
∴CD=AD,故①正确;
②连接OC,
由①知:OM'是AC的垂直平分线,∴OC=OA,
∴OA=OB=OC,
以O为圆心,以OA为半径作⊙O,交AO的延长线于E,连接BE,
则A、B、C都在⊙O上,
∵∠MON=120°,
∴∠BOE=60°,
∵OB=OE,
∴△OBE是等边三角形,
∴∠E=60°,
∵A、C、B、E四点共圆,
∴∠ACD=∠E=60°,故②不正确;
③当α=30°时,即∠AOD=∠COD=30°,
∴∠AOC=60°,
∴△AOC是等边三角形,
∴∠OAC=60°,OC=OA=AC,
由①得:CD=AD,
∴∠CAD=∠ACD=∠CDA=60°,
∴△ACD是等边三角形,
∴AC=AD=CD,
∴OC=OA=AD=CD,
∴四边形OADC为菱形,故③正确;
④∵CD=AD,∠ACD=60°,
∴△ACD是等边三角形,
当AC最大时,△ACD的面积最大,
∵AC是⊙O的弦,即当AC为直径时最大,此时AC=2OA=2a,α=90°,
∴△ACD面积的最大值是:![]() AC2=
AC2=![]() ,故④正确,
,故④正确,
所以本题结论正确的有:①③④,
故答案为:①③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程2x2+2x﹣1=0的两个根为x1,x2,且x1<x2,下列结论正确的是( )
A. x1+x2=1 B. x1x2=﹣1 C. |x1|<|x2| D. x12+x1=

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个图案均由边长相等的黑、白两色正力形按规律拼接面成,照此规律,第n个图案中白色正方形比黑色正方形( )个.

A.nB.(5n+3)C.(5n+2)D.(4n+3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在
 处,
处, 交AD于点E.
交AD于点E.(1)试判断△BDE的形状,并说明理由;
(2)若
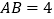 ,
,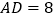 ,求△BDE的面积.
,求△BDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为110m,那么该建筑物的高度BC约为_____m(结果保留整数,
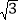 ≈1.73).
≈1.73).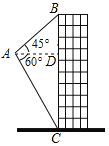
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣
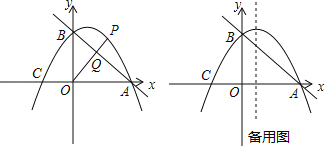
x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣ x2+bx+c经过A、B两点,与x轴的另一个交点为C.
x2+bx+c经过A、B两点,与x轴的另一个交点为C.(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的点,连接OP交直线AB于点Q.设点P的横坐标为m,PQ与OQ的比值为y,求y与m的关系式,并求出PQ与OQ的比值的最大值;
(3)点D是抛物线对称轴上的一动点,连接OD、CD,设△ODC外接圆的圆心为M,当sin∠ODC的值最大时,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2
 ,求FH的长.
,求FH的长.
相关试题

