【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )

A. ②③ B. ③④ C. ①②④ D. ②③④
参考答案:
【答案】D
【解析】∵矩形ABCD,
∴AD∥BC,![]() ,AO=OC,OD=OB,AC=BD,
,AO=OC,OD=OB,AC=BD,
∴AO=OB=OD,
∵AB=1,AD=![]() ,由勾股定理得:AC=2,
,由勾股定理得:AC=2,
∴∠ABD=60°,
∴△ABO是等边三角形,
∴AB=OA=OB, ∠BAO=∠AOB=60°,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵∠DAF=∠AFB,
∴∠BAF=∠BFA,![]() ,∴②正确;
,∴②正确;
∵CE⊥BD,![]() ,
,
∴∠ECO=30°,![]() ,
,![]() ,
,
∴AC=CH, ∴③正确;
∵CF和AH不垂直, ∴AF≠FH, ∴①错误;
∵∠CEO=90°, ∠ECA=30°,![]() ,
,
BE=3DE, ∴④正确.
正确的有②③④,故选D.
点睛;本题主要考查对等腰三角形的性质,勾股定理,三角形的外角性质,矩形的性质,平行线的性质,等边三角形的性质和判定等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,三边分别为下列长度,判断该三角形是不是直角三角形,并指出哪一个角是直角.
(1)a=
 ,b=2
,b=2 ,c=
,c= ;
;(2)a=5,b=7,c=9;
(3)a=2,b=
 ,c=
,c= ;
;(4)a=5,b=2
 ,c=1.
,c=1. -
科目: 来源: 题型:
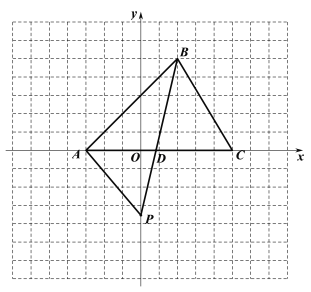
查看答案和解析>>【题目】(如图平面直角坐标系内,已知点A的坐标是(-3,0).
(1)点B的坐标为_______,点C的坐标为_____,∠BAC=______;
(2)求△ABC的面积;
(3)点P是y轴负半轴上的一个动点,连接BP交
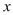 轴于点D,是否存在点P使得
轴于点D,是否存在点P使得△ADP与△BC的面积相等?若存在,请直接写出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,CD⊥AB,垂足为D,如果CD=12,AD=16,BD=9,那么△ABC是直角三角形吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有点
 ,点
,点 第一次跳动至带你
第一次跳动至带你 ,第二次点
,第二次点 跳动至带你
跳动至带你 ,第三次点
,第三次点 跳动至带你
跳动至带你 ,第四次点
,第四次点 跳动至带你
跳动至带你 ,…… 依此规律跳动下去,则点
,…… 依此规律跳动下去,则点 与点
与点 之间的距离是( )
之间的距离是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为m(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC ;
(2)若∠BAC=
 ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.
相关试题

