【题目】已知关于x的一元二次方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)若方程的两个根的平方和等于5,求k的值.
参考答案:
【答案】(1)详见解析;(2):k=±1.
【解析】
(1)根据方程的系数结合根的判别式,可得出△=(2k﹣1)2≥0,由此可证出:无论k取任何实数时(k≠0),方程总有实数根;
(2)根据根与系数的关系可得x1+x2=﹣![]() 、x1x2=
、x1x2=![]() ,结合x12+x22=5即可得出关于k的一元二次方程,解之即可得出k值.
,结合x12+x22=5即可得出关于k的一元二次方程,解之即可得出k值.
(1)证明:∵方程kx2+(2k+1)x+2=0为一元二次方程,
∴k≠0.
∵△=(2k+1)2﹣4×2k=(2k﹣1)2≥0,
∴无论k取任何实数时(k≠0),方程总有实数根;
(2)解:设方程kx2+(2k+1)x+2=0的两个根为x1、x2,
∴x1+x2=﹣![]() ,x1x2=
,x1x2=![]() .
.
∵x12+x22=(x1+x2)2﹣2x1x2=5,即(﹣![]() )2﹣
)2﹣![]() =5,
=5,
整理,得:k2=1,
解得:k=±1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90,∠B=30,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于
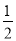 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,
(1)判断下列命题的真假
①AD是△ABC的角平分线 ( )
②点D在AB的中垂线上 ( )
③S△ADC:S△ADB=1:2( )
(2)从(1)的②③两个命题中,选择一个真命题,写出证明。
-
科目: 来源: 题型:
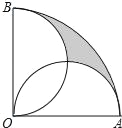
查看答案和解析>>【题目】如图,在半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )

A. 14 B. 16 C. 17 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=13,点A、B的坐标分别为(1,0),(6,0),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣4上时,线段BC扫过的面积为( )

A.84B.80C.91D.78
-
科目: 来源: 题型:
查看答案和解析>>【题目】“品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别
成绩x(分)
人数
百分比
A
60≤x<70
8
20%
B
70≤x<80
16
m%
C
80≤x<90
a
30%
D
90≤<x≤100
4
10%
请观察图表,解答下列问题:
(1)表中a= ,m= ;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】今年春北方严重干旱,某社区人畜饮水紧张,每天需从社区外调运饮用水120吨,有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨,从两水厂运水到社区供水点的路程和运费如下表:
到社区供水点的路程(千米)
运费(元/吨·千米)
甲厂
20
12
乙厂
14
15
【1】若某天调运水的总运费为26700元,则从甲、乙两水厂各调运多少吨饮用水?
【2】设从甲厂调运饮用水
 吨,总运费为W元,试写出W关于与
吨,总运费为W元,试写出W关于与 的函数关系式,怎样安排调运方案才能使每天的总运费最省?
的函数关系式,怎样安排调运方案才能使每天的总运费最省?
相关试题

