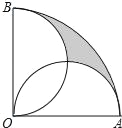
【题目】如图,在半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为_____.
参考答案:
【答案】![]() ﹣1.
﹣1.
【解析】
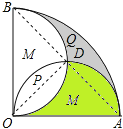
试题假设出扇形半径,再表示出半圆面积,以及扇形面积,进而即可表示出两部分P,Q面积相等.连接AB,OD,根据两半圆的直径相等可知∠AOD=∠BOD=45°,故可得出绿色部分的面积=S△AOD,利用阴影部分Q的面积为:S扇形AOB﹣S半圆﹣S绿色,故可得出结论.
解:∵扇形OAB的圆心角为90°,扇形半径为2,
∴扇形面积为:![]() =π(cm2),
=π(cm2),
半圆面积为:![]() ×π×12=
×π×12=![]() (cm2),
(cm2),
∴SQ+SM =SM+SP=![]() (cm2),
(cm2),
∴SQ=SP,
连接AB,OD,
∵两半圆的直径相等,
∴∠AOD=∠BOD=45°,
∴S绿色=S△AOD=![]() ×2×1=1(cm2),
×2×1=1(cm2),
∴阴影部分Q的面积为:S扇形AOB﹣S半圆﹣S绿色=π﹣![]() ﹣1=
﹣1=![]() ﹣1(cm2).
﹣1(cm2).
故答案为:![]() ﹣1.
﹣1.
-
科目: 来源: 题型:
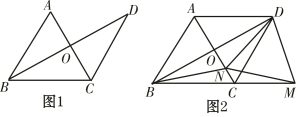
查看答案和解析>>【题目】已知,△ABC是等边三角形,过点C作CD∥AB,且CD=AB,连接BD交AC于点O.
(1)如图1,求证:AC垂直平分BD;
(2)如图2,点M在BC的延长线上,点N在线段CO上,且ND=NM,连接BN.求证:NB=NM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕点P旋转时,下列结论①EF=AP;②△EPF为等腰直角三角形;③AE=CF;④S四边形AEPF
 ,正确的有( )
,正确的有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90,∠B=30,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于
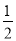 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,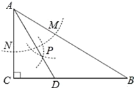
(1)判断下列命题的真假
①AD是△ABC的角平分线 ( )
②点D在AB的中垂线上 ( )
③S△ADC:S△ADB=1:2( )
(2)从(1)的②③两个命题中,选择一个真命题,写出证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )

A. 14 B. 16 C. 17 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)若方程的两个根的平方和等于5,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=13,点A、B的坐标分别为(1,0),(6,0),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣4上时,线段BC扫过的面积为( )

A.84B.80C.91D.78
相关试题

