【题目】正方形ABCD的边长为4,将此正方形置于平面直角坐标系中,使AB边落在X轴的正半轴上,且A点的坐标是(1,0).
(1)直线![]() 经过点C,且与x轴交与点E,求四边形AECD的面积;
经过点C,且与x轴交与点E,求四边形AECD的面积;
(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的解析式;
(3)若直线l1经过点F(﹣![]() ,0),且与直线y=3x平行,将(2)中直线l沿着y轴向上平移
,0),且与直线y=3x平行,将(2)中直线l沿着y轴向上平移![]() 个单位交轴x于点M,交直线l1于点N,求△NMF的面积.
个单位交轴x于点M,交直线l1于点N,求△NMF的面积.

参考答案:
【答案】(1)四边形AECD在面积为10;(2)直线l的解析式为y=2x-4;(3)![]()
【解析】试题分析:(1)由题意知边长已经告诉,易求四边形的面积;
(2)直线l经过点E且将正方形ABCD分成面积相等的两部分,设与DC交于点F,根据正方形的性质,可求出F点坐标,设直线l的解析式是y=kx+b,把E、F的坐标代入即可求出解析式;
(3)根据直线l1经过点F(﹣![]() ,0)且与直线y=3x平行,知k=3,把F的坐标代入即可求出b的值即可得出直线11,同理求出解析式y=2x-3,进一步求出M、N的坐标,利用三角形的面积公式即可求出△MNF的面积.
,0)且与直线y=3x平行,知k=3,把F的坐标代入即可求出b的值即可得出直线11,同理求出解析式y=2x-3,进一步求出M、N的坐标,利用三角形的面积公式即可求出△MNF的面积.
试题解析:(1)在y=![]() x
x![]() 中,令y=4,即
中,令y=4,即![]() x
x![]() =4,解得:x=5,则B的坐标是(5,0);
=4,解得:x=5,则B的坐标是(5,0);
令y=0,即![]() x
x![]() =0,解得:x=2,则E的坐标是(2,0).
=0,解得:x=2,则E的坐标是(2,0).
则OB=5,OE=2,BE=OB﹣OA=5﹣2=3,∴AE=AB﹣BE=4﹣3=1,
四边形AECD的面积=![]() (AE+CD)AD=
(AE+CD)AD=![]() (4+1)×4=10;
(4+1)×4=10;
(2)经过点E且将正方形ABCD分成面积相等的两部分,则直线与CD的交点F,必有CF=AE=1,则F的坐标是(4,4).
设直线的解析式是y=kx+b,则![]() ,解得:
,解得: ![]() .
.
则直线l的解析式是:y=2x﹣4;
(3)∵直线l1经过点F(﹣![]() ,0)且与直线y=3x平行,
,0)且与直线y=3x平行,
设直线11的解析式是y1=kx+b,则:k=3,
代入得:0=3×(﹣![]() )+b,解得:b=
)+b,解得:b=![]() ,
,
∴y1=3x+![]() ,
,
已知将(2)中直线l沿着y轴向上平移![]() 个单位,则所得的直线的解析式是y=2x﹣4+
个单位,则所得的直线的解析式是y=2x﹣4+![]() ,
,
即:y=2x﹣3![]() ,当y=0时,x=
,当y=0时,x=![]() ,∴M(
,∴M(![]() ,0),
,0),
解方程组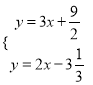 得:
得: 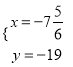 ,即:N(﹣7
,即:N(﹣7![]() ,﹣19),
,﹣19),
S△NMF=![]() ×[
×[![]() ﹣(﹣
﹣(﹣![]() )]×|﹣19|=
)]×|﹣19|=![]() .
.
答:△NMF的面积是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近两年,国际市场黄金价格涨幅较大,中国交通银行推出“沃德金”的理财产品,即以黄金为投资产品,投资者从黄金价格的上涨中赚取利润.上周五黄金的收盘价为285元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六.星期日休市)
星期
一
二
三
四
五
收盘价的变化(与前一天收盘价比较)
+7
+5
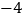
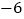
+8
问:(1)本周星期三黄金的收盘价是多少?
(2)本周黄金收盘时的最高价.最低价分别是多少?
(3)上周,小王以周五的收盘价285元/克买入黄金1000克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金1000克,他的收益情况如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:O是直线AB上的一点,
 是直角,OE平分
是直角,OE平分 .
.(1)如图1.若
 .求
.求 的度数;
的度数;(2)在图1中,
 ,直接写出
,直接写出 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);(3)将图1中的
 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究 和
和 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将自然数按如表规律排列,表中数2在第二行第一列,与有序数对
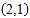 对应,数5与
对应,数5与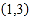 对应,数14与
对应,数14与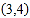 对应,根据这一规律,数2014对应的有序数对为__________.
对应,根据这一规律,数2014对应的有序数对为__________.第一列
第二列
第三列
第四列
第五列
第一行
1
4
5
16
17
…
第二行
2
3
6
15
…
第三行
9
8
7
14
…
第四行
10
11
12
13
…
第五行
…
……
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织学生到距离学校6千米的科技馆去参观,小华因事没能乘上学校的包车,于是准备在学校门口改乘出租车去科技馆,出租车收费标准有两种类型,如下表:
里程
甲类收费(元)
乙类收费(元)
3千米以下(包含3千米)
7.00
6.00
3千米以上,每增加1千米
1.60
1.40
(1)设出租车行驶的里程为x千米(
 且x取正整数),分别写出两种类型的总收费(用含x的代数式表示);
且x取正整数),分别写出两种类型的总收费(用含x的代数式表示);(2)小华身上仅有11元,他乘出租车到科技馆车费够不够请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AD∥BC,BC=20cm,AD=10cm,现有两个动点P、Q分别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10).
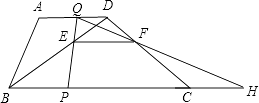
(1)当t为何值时,四边形PCDQ为平行四边形?
(2)在P、Q移动的过程中,线段PH的长是否发生改变?如果不变,求出线段PH的长;如果改变,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】近两年,国际市场黄金价格涨幅较大,中国交通银行推出“沃德金”的理财产品,即以黄金为投资产品,投资者从黄金价格的上涨中赚取利润.上周五黄金的收盘价为285元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六.星期日休市)
星期
一
二
三
四
五
收盘价的变化(与前一天收盘价比较)
+7
+5


+8
问:(1)本周星期三黄金的收盘价是多少?
(2)本周黄金收盘时的最高价.最低价分别是多少?
(3)上周,小王以周五的收盘价285元/克买入黄金1000克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金1000克,他的收益情况如何?
相关试题

