【题目】在平面直角坐标系中,正方形![]() 的点
的点![]() ,
,![]() ,
,![]() ,现将此正方形绕
,现将此正方形绕![]() 逆时针旋转
逆时针旋转![]() ,得到正方形
,得到正方形![]() ,求正方形
,求正方形![]() 各顶点的坐标.
各顶点的坐标.
参考答案:
【答案】![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
作A1D⊥x轴于D,C1E⊥x轴于E,如图,根据正方形的性质得OB=2![]() ,∠BOA=∠BOC=45°,再根据旋转的性质得点B1在y轴上,OB1=OB=2
,∠BOA=∠BOC=45°,再根据旋转的性质得点B1在y轴上,OB1=OB=2![]() ,∠A1OD=45°,∠B1OC1=45°,OA1=OA=OC1=2,则可判断△A1OD和△EOC1都是等腰直角三角形,于是可根据等腰直角三角形的性质得到A1D=OD=
,∠A1OD=45°,∠B1OC1=45°,OA1=OA=OC1=2,则可判断△A1OD和△EOC1都是等腰直角三角形,于是可根据等腰直角三角形的性质得到A1D=OD=![]() OA1=
OA1=![]() ,C1E=OE=
,C1E=OE=![]() OC1=
OC1=![]() ,然后根据各象限点的坐标特征和y轴上点的坐标特征写出正方形OA1B1C1各顶点的坐标.
,然后根据各象限点的坐标特征和y轴上点的坐标特征写出正方形OA1B1C1各顶点的坐标.
解:作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,如图,
,如图,
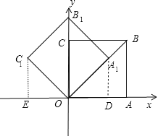
∵正方形![]() 的点
的点![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴正方形![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() ,得到正方形
,得到正方形![]() ,
,
∴点![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克)
…
34.8
32
29.6
28
…
售价 x(元/千克)
…
22.6
24
25.2
26
…
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是用围棋子摆出的图案(用棋子的位置用用有序数对表示,如
 点在
点在 ),如果再摆一黑一白两枚棋子,使
),如果再摆一黑一白两枚棋子,使 枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )
枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )
A. 黑(3,3),白(3,1) B. 黑(3,1),白(3,3)
C. 黑(1,5),白(5,5) D. 黑(3,2),白(3,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=62°,∠ACB=29°,求∠FGC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)设计费能达到24000元吗?为什么?
(3)当x是多少米时,设计费最多?最多是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
(1)求直线OA和二次函数的解析式;
(2)当点P在直线OA的上方时,
①当PC的长最大时,求点P的坐标;
②当S△PCO=S△CDO时,求点P的坐标.


-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次“构造勾股数”的探究性学习中,老师给出了下表:

其中m、n为正整数,且m>n.
(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.
(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a=___,b=___,c=___.
(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.
相关试题

