【题目】云南地区地震发生后,市政府筹集了必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)

(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能求出这三种车型分别有多少辆吗?此时的运费又是多少元?
参考答案:
【答案】(1)需要甲种车型8辆,一种车型10辆;
(2)甲车2辆,乙车5辆,丙车7辆,需运费7500元。
【解析】试题分析:(1)首先设需要甲种车型x辆,一种车型y辆,由题意得等量关系:①运费8200元;②运送物资120吨,根据等量关系列出方程组即可;(2)设甲车有a辆,乙车有b辆,则丙车有(14-a-b)辆,由题意得方程5a+8b+10(14-a-b)=120,再计算出整数解即可.
试题解析:(1)设需要甲种车型x辆,一种车型y辆,由题意得:
![]() ,
,
解得: ![]() .
.
答:需要甲种车型8辆,一种车型10辆;
(2)设甲车有a辆,乙车有b辆,则丙车有(14ab)辆,由题意得:
5a+8b+10(14ab)=120,
化简得5a+2b=20,
即a=425b,
∵a、b、14ab均为正整数,
∴b只能等于5,从而a=2,14ab=7,
∴甲车2辆,乙车5辆,丙车7辆,
∴需运费400×2+500×5+600×7=7500(元),
答:甲车2辆,乙车5辆,丙车7辆,需运费7500元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式,且把结果化为只含有正整数指数的形式:
(1)(x﹣2)﹣3(yz﹣1)3 ;(2)a2b3(2a﹣1b)3
(3)(3a3b2c﹣1)﹣2(5ab﹣2c3)2;(4)
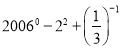 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是AB上一点,DF交AC于点E,AE=EC,DE=EF,则下列说法中:①∠ADE=∠EFC;②∠ADE+∠ECF+∠FEC=180°;③∠B+∠BCF=180°;④S△ABC=S四边形DBCF.正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂设计了一款工艺品,每件成本
 元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是
元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是 元时,每天的销售量是
元时,每天的销售量是 件,若销售单价每降低
件,若销售单价每降低 元,每天就可多售出
元,每天就可多售出 件,但要求销售单价不得低于
件,但要求销售单价不得低于 元.如果降价后销售这款工艺品每天能盈利
元.如果降价后销售这款工艺品每天能盈利 元,那么此时销售单价为多少元?
元,那么此时销售单价为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,BC=6,AC=4.点P、Q分别从点A、B同时出发,点P沿A→C的方向以每秒1个单位长的速度向点C运动,点Q沿B→C的方向以每秒2个单位长的速度向点C运动.当其中一个点先到达点C时,点P、Q停止运动.当四边形ABQP的面积是△ABC面积的一半时,求点P运动的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线CF,标出F点;
(2)过点B画AC的垂线BG,垂足为点G,标出G点;
(3)点B到AC的距离是线段 的长度;
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .

相关试题

