【题目】如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4m.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2m的通道,试判断距离B点4m的货物MNQP是否需要挪走,并说明理由.(结果精确到0.01m,已知![]() )
)

参考答案:
【答案】(1)AC的长度约为5.6m;(2)货物MNQP需要挪走,理由见解析
【解析】(1)过A作BC的垂线AD.在构建的直角三角形中,首先求出两个直角三角形的公共直角边,进而在Rt△ACD中,求出AC的长.
(2)通过解直角三角形,可求出BD、CD的长,进而可求出BC、PC的长.然后判断PC的值是否大于2米即可.
解:(1)过点A作AD⊥BC于D,在Rt△ABD中,
AD=ABSin45°=![]()
在Rt△ABD中,∵∠ACD=30° ∴AC=2AD=![]()
答:新传送带AC的长度约为5.6m
(2)在Rt△ABD中,BD=ABCOS45°=![]()
在Rt△ACD中,CD=ABCOS30°=![]()
∴CB=CD-BD=![]()
∵PC=PB-CB![]()
∴货物MNQP需要挪走
“点睛”本题考查了解直角三角形的应用,注意应用问题尽管题型千变万化,但关键是设法化归为解直角三角形问题,必要时应添加辅助线,构造出直角三角形.在两个直角三角形有公共直角边时,先求出公共边的长是解答此类题的基本思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一台自动测温记录仪的图象,它反映了嵊州市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
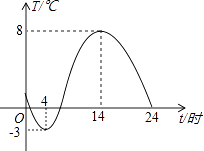
A.凌晨4时气温最低为﹣3℃
B.从0时至14时,气温随时间增长而上升
C.14时气温最高为8℃
D.从14时至24时,气温随时间增长而下降 -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列运算:81=8,82=64,83=512,84=4096,85=32768,86=262144,…,则81+82+83+84+…+82014的和的个位数字是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,使点B落在点E处,连结DE,若DE:AC=3:5,则
 的值为___.
的值为___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校举行“阳光少年,励志青春”的演讲比赛中,五位评委给选手小明的平分分别为:90,85,90,80,95,则这组数据的众数是( )
A. 95 B. 90 C. 85 D. 80
-
科目: 来源: 题型:
查看答案和解析>>【题目】运算与推理以下是甲、乙两人得到
 +
+  >
>  的推理过程:(甲)因为
的推理过程:(甲)因为  >
>  =3,
=3,  >
>  =2,所以
=2,所以  +
+  >3+2=5.又
>3+2=5.又  =
=  <
<  =5,所以
=5,所以  +
+  >
>  .(乙)作一个直角三角形,两直角边长分别为
.(乙)作一个直角三角形,两直角边长分别为  ,
,  .利用勾股定理得斜边长的平方为
.利用勾股定理得斜边长的平方为  ,所以
,所以  +
+  >
>  .对于两个人的推理,下列说法中正确的是( )
.对于两个人的推理,下列说法中正确的是( )
A.两人都正确
B.两人都错误
C.甲正确,乙错误
D.甲错误,乙正确 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果等腰三角形的每条边长都是方程x2﹣5x+4=0的解,那么它的周长为___
相关试题

