【题目】郊区某中学学霸父母只要有时间就陪孩子一起完成家庭作业,在某天晚上,勤芬准备完成作业时:化简(![]() x2+7x+6)﹣(7x+8x2﹣4).发现系数“
x2+7x+6)﹣(7x+8x2﹣4).发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)她把“![]() ”猜成3,请你化简:(3x2+7x+6)﹣(7x+8x2﹣4);
”猜成3,请你化简:(3x2+7x+6)﹣(7x+8x2﹣4);
(2)爸爸说:“你猜错了,我看了标准答案的结果是常数.”请你通过计算说明来帮助勤芬得到原题中“![]() ”是几.
”是几.
参考答案:
【答案】(1)﹣5x2+10;(2)原题中的数为8.
【解析】
(1)去括号,合并同类项即可得解;
(2)设看不清的数字为a,然后去括号合并同类项,再由结果为常数,即可得出a.
(1)原式=3x2+7x+6﹣7x﹣8x2+4
=﹣5x2+10;
(2)设看不清的数字为a,
则原式=(ax2+7x+6)﹣(7x+8x2﹣4)
=ax2+7x+6﹣7x﹣8x2+4
=(a﹣8)x2+10;
因为结果为常数,所以a﹣8=0,
解得:a=8
即原题中的数为8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高市民的精神生活美化城市环境,城市管理局从外地新进一批绿化树苗,现有两种运输方式可供选择,
方式一:使用快递公司的邮车运输,装卸收费500元,另外每公里再加收5元;
方式二:使用铁路运输公司的火车运输,装卸收费900元,另外每公里再加收3元.
(1)请分别写出邮车、火车运输的总费用为
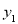 (元)、
(元)、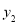 (元)与运输路程
(元)与运输路程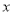 (公里)之间的函数关系式;
(公里)之间的函数关系式;(2)你认为选用哪种运输方式较好,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设
 ,
,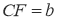 ,满足
,满足 .
.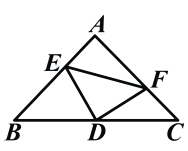
(1)求BE及CF的长。
(2)求证:
 。
。(3)在(1)的条件下,求△DEF的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连结BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.
(1)求证:DF⊥AB;
(2)利用图中阴影部分面积完成勾股定理的证明,已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,求证:a2+b2=c2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列一段文字,再解答问题
已知在平面内有两点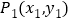 ,
,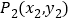 ,其两点间的距离公式为
,其两点间的距离公式为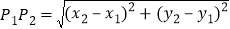 ,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为
,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为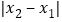 或
或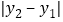
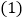 已知点
已知点 ,
,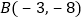 ,试求A,B两点间的距离;
,试求A,B两点间的距离; 已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为
已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为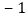 ,试求A,B两点间的距离;
,试求A,B两点间的距离;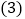 已知点
已知点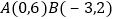 ,
,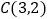 ,判断线段AB,BC,AC中哪两条是相等的?并说明理由.
,判断线段AB,BC,AC中哪两条是相等的?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题)先阅读下列一段文字,然后解答问题:
已知:方程
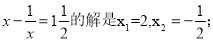
方程
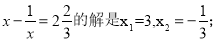
方程
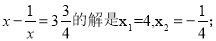
方程
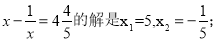
问题:观察上述方程及其解,再猜想出方程:
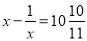 的解,并试着解分式方程验证.
的解,并试着解分式方程验证.【答案】
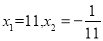
【解析】试题分析:首先通过观察发现,它的规律是:方程x
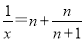 的解为x1=n+1,x2=
的解为x1=n+1,x2=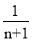 ,利用这个规律就可以求出方程的解.
,利用这个规律就可以求出方程的解.试题解析:∵
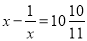
∴x2-11x-120=0
解得:
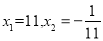 .
.【题型】解答题
【结束】
20【题目】(2017北京市)关于x的一元二次方程
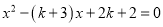 .
.(1)求证:方程总有两个实数根;
(2)若方程有一根小于1,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BC=8,tanB=
 ,点D是AB的中点,如果把△BCD沿直线CD翻折,使得点B落在同一平面内的B′处,联结A B′,那么A B′的长为_____.
,点D是AB的中点,如果把△BCD沿直线CD翻折,使得点B落在同一平面内的B′处,联结A B′,那么A B′的长为_____.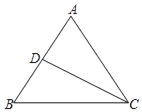
相关试题

