【题目】(如图(1),在矩形ABCD中,AB=4,BC=3,点E是射线CD上的一个动点,把△BCE沿BE折叠,点C的对应点为F.
(1)若点F刚好落在线段AD的垂直平分线上时,求线段CE的长;
(2)若点F刚好落在线段AB的垂直平分线上时,求线段CE的长;
(3)当射线AF交线段CD于点G时,请直接写出CG的最大值 .


参考答案:
【答案】(1)CE=![]() ;(2)CE=
;(2)CE=![]() ;(3)CG的最大值是4-
;(3)CG的最大值是4-![]()
【解析】(1)根据垂直平分线的性质,等边三角形的性质求出即可;(2)利用垂直平分线的性质得出FE=EC ,再利用相似三角形的性质进而得出答案;(3)当射线AF交线段CD于点G时求出即可.
解: ∵点F刚好落在线段AD的垂直平分线上,∴FB=FC.
∵折叠 ,∴FB=BC=3.
∴△FBC是等边三角形,∴∠FBC=60°, ∠EBC=30°.
在Rt△EBC,∴CE=![]() BC=
BC=![]() .
.
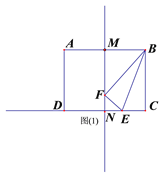
(2)如图(1)∵点F刚好落在线段AB的垂直平分线MN上,
∵折叠,∴FE=EC.
∴BM=2,在Rt△MFB中,MF=![]() .
.
∵△MBF∽△NFE,
∴![]() =
=![]() .
.
∴CE=EN=![]() .
.
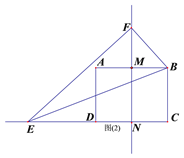
如图(2)∵折叠 ,∴FE=EC.
同理MF=![]() ,FN=3+
,FN=3+![]() .
.
∵△MBF∽△NFE,∴![]() =
=![]() .
.
∴CE=EN=![]() .
.
(3)CG的最大值是4-![]() .
.
“点睛”此题主要考查了垂直平分线、等边三角形、矩形的性质、翻折变换的性质、相似三角形等知识;利用数形结合以及分类讨论得出是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的关系是___;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于函数
 的四个命题:①当
的四个命题:①当 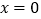 时,
时,  有最小值10;②
有最小值10;②  为任意实数,
为任意实数,  时的函数值大于
时的函数值大于  时的函数值;③若
时的函数值;③若  ,且
,且  是整数,当
是整数,当  时,
时,  的整数值有
的整数值有  个;④若函数图象过点
个;④若函数图象过点  和
和  ,其中
,其中  ,
,  ,则
,则  .其中真命题的序号是( )
.其中真命题的序号是( )
A.①
B.②
C.③
D.④ -
科目: 来源: 题型:
查看答案和解析>>【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).
①如图1,若BC=4m,则S=m.
②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变.则在BC的变化过程中,当S取得最小值时,边BC的长为m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为为50m.设饲养室长为x(m),占地面积为y(m2).

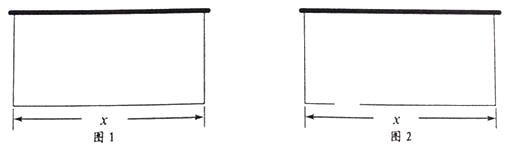
(1)如图1,问饲养室长x为多少时,占地面积y最大?
(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大。小敏说:“只要饲养室长比(1)中的长多2m就行了.” -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )

A、120° B、135° C、150° D、45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日的钱塘江观潮信息如表:


按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离 (千米)与时间
(千米)与时间  (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点  ,点
,点  坐标为
坐标为  ,曲线
,曲线  可用二次函数
可用二次函数  (
(  ,
,  是常数)刻画.
是常数)刻画.
(1)求 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度  ,
,  是加速前的速度).
是加速前的速度).
相关试题

