【题目】如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则 ![]() 的值为 .
的值为 . 
参考答案:
【答案】![]()
【解析】解:∵矩形沿直线AC折叠,点B落在点E处,
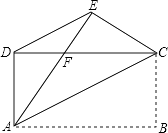
∴∠BAC=∠EAC,AE=AB=CD,
∵矩形ABCD的对边AB∥CD,
∴∠DCA=∠BAC,
∴∠EAC=∠DCA,
设AE与CD相交于F,则AF=CF,
∴AE﹣AF=CD﹣CF,
即DF=EF,
∴ ![]() =
= ![]() ,
,
又∵∠AFC=∠EFD,
∴△ACF∽△EDF,
∴ ![]() =
= ![]() =
= ![]() ,
,
设DF=3x,FC=5x,则AF=5x,
在Rt△ADF中,AD= ![]() =
= ![]() =4x,
=4x,
又∵AB=CD=DF+FC=3x+5x=8x,
∴ ![]() =
= ![]() =
= ![]() .
.
故答案为: ![]() .
.
根据翻折的性质可得∠BAC=∠EAC,再根据矩形的对边平行可得AB∥CD,根据两直线平行,内错角相等可得∠DAC=∠BCA,从而得到∠EAC=∠DAC,设AE与CD相交于F,根据等角对等边的性质可得AF=CF,再求出DF=EF,从而得到△ACF和△EDF相似,根据相似三角形对应边成比例
设DF=3x,FC=5x,在Rt△ADF中,利用勾股定理列式求出AD,再根据矩形的对边相等求出AB,然后代入进行计算即可得到所求的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1和l2于B、C两点,连接AC、BC,若∠ABC=65°,则∠1的度数是( )

A. 35° B. 50° C. 65° D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的一条边与另一条边的反向延长线组成的角,叫做三角形的外角。如图,点D为BC延长线上一点,则∠ACD为△ABC的一个外角。
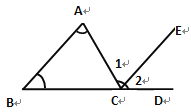
求证:∠ACD=∠A+∠B
证明:过点C作CE∥AB(过直线外一点 )
∴∠B= ( )
∠A= ( )
∵∠ACD=∠1+∠2
∴∠ACD=∠ +∠B(等量代换)
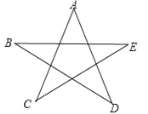
应用:如图是一个五角星,请利用上述结论求
∠A+∠B+∠C+∠D+∠E的值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.

A.4 B.3 C.2 D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织了一次防溺水、防交通事故、防食物中毒、防校园欺凌及其他各种安全意识的调查活动,了解同学们在哪些方面的安全意识薄弱,便于今后更好地开展安全教育活动.根据调查结果,绘制出图1,图2两幅不完整的统计图.
请结合图中的信息解答下列问题: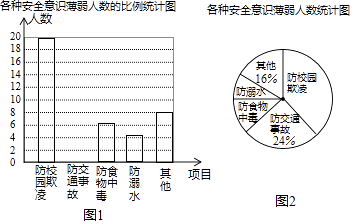
(1)本次调查的人数为 , 其中防校园欺凌意识薄弱的人数占%;
(2)补全条形统计图;
(3)若该校共有1500名学生,请估计该校学生中防溺水意识薄弱的人数;
(4)请你根据题中的信息,给该校的安全教育提一个合理的建议. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.
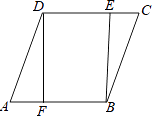
(1)求证:AF=CE;
(2)若DE=2,BE=4,求sin∠DAF的值.
相关试题

