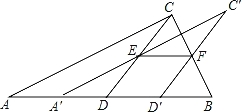
【题目】(2016湖南省邵阳市第10题)如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
参考答案:
【答案】△A′DE是等腰三角形;证明过程见解析.
【解析】
试题分析:当四边形EDD′F为菱形时,△A′DE是等腰三角形,△A′DE≌△EFC′.先证明CD=DA=DB,得到∠DAC=∠DCA,由AC∥A′C′即可得到∠DA′E=∠DEA′由此即可判断△DA′E的形状.由EF∥AB推出∠CEF=∠EA′D,∠EFC=∠A′D′C=∠A′DE,再根据A′D=DE=EF即可证明.
试题解析:当四边形EDD′F为菱形时,△A′DE是等腰三角形,△A′DE≌△EFC′.
理由:∵△BCA是直角三角形,∠ACB=90°,AD=DB, ∴CD=DA=DB, ∴∠DAC=∠DCA,
∵A′C∥AC, ∴∠DA′E=∠A,∠DEA′=∠DCA, ∴∠DA′E=∠DEA′, ∴DA′=DE,
∴△A′DE是等腰三角形. ∵四边形DEFD′是菱形, ∴EF=DE=DA′,EF∥DD′,
∴∠CEF=∠DA′E,∠EFC=∠CD′A′, ∵CD∥C′D′, ∴∠A′DE=∠A′D′C=∠EFC,
在△A′DE和△EFC′中,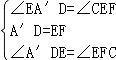 , ∴△A′DE≌△EFC′.
, ∴△A′DE≌△EFC′.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(﹣1,0),点B(0,﹣2),AD与y轴交于点E,且E为AD的中点,双曲线y=
 经过C,D两点且D(a,4)、C(2,b).
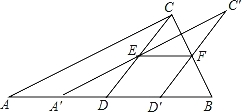
经过C,D两点且D(a,4)、C(2,b).(1)求a、b、k的值;
(2)如图2,线段CD能通过旋转一定角度后点C、D的对应点C′、D′还能落在y=
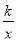 的图象上吗?如果能,写出你是如何旋转的,如果不能,请说明理由;
的图象上吗?如果能,写出你是如何旋转的,如果不能,请说明理由;(3)如图3,点P在双曲线y=
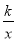 上,点Q在y轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试求满足要求的所有点P、Q的坐标.
上,点Q在y轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试求满足要求的所有点P、Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣4x的图象的顶点坐标是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,不正确的是( )
A.在同一平面内,过一点有而且只有一条直线与已知直线垂直
B.经过直线外一点,有而且只有一条直线与这条直线平行
C.垂直于同一直线的两条直线垂直
D.平行于同一直线的两条直线平行 -
科目: 来源: 题型:
查看答案和解析>>【题目】果品店刚试营业,就在批发市场购买某种水果销售,第一次用500元购进若干千克水果,并以每千克定价7元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了20%,用660元所购买的数量比第一次多10千克.仍以原来的单价卖完.
求第一次该种水果的进价是每千克多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠DAB=60°,点E、F分别在CD、AB的延长线上,且AE=AD,CF=CB.
(1)求证:四边形AFCE是平行四边形;
(2)若去掉已知条件的“∠DAB=60°”,上述的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出下列已知点关于原点对称点的坐标.
A(-2,3) B(5,-5) C(-3,-7) D(3,-2) E(4,6)
相关试题

