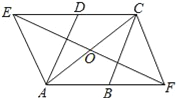
【题目】如图,在ABCD中,∠DAB=60°,点E、F分别在CD、AB的延长线上,且AE=AD,CF=CB.
(1)求证:四边形AFCE是平行四边形;
(2)若去掉已知条件的“∠DAB=60°”,上述的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.
参考答案:
【答案】(1)(2)见解析
【解析】(1)由已知条件可得△AED,△CFB是正三角形,可得∠AEC=∠BFC=60°,∠EAF=∠FCE=120°,所以四边形AFCE是平行四边形.
(2)上述结论还成立,可以证明△ADE≌△CBF,可得∠AEC=∠BFC,∠EAF=∠FCE,所以四边形AFCE是平行四边形.
解:(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,∠DCB=∠DAB=60°.
∴∠ADE=∠CBF=60°.
∵AE=AD,CF=CB,
∴△AED,△CFB是正三角形.
∴∠AEC=∠BFC=60°,∠EAF=∠FCE=120°.
∴四边形AFCE是平行四边形.
(2)解:上述结论还成立.
证明:∵四边形ABCD是平行四边形,
∴DC∥AB,∠CDA=∠CBA,∠DCB=∠DAB,AD=BC,DC=AB.
∴∠ADE=∠CBF.
∵AE=AD,CF=CB,
∴∠AED=∠ADE,∠CFB=∠CBF.
∴∠AED=∠CFB.
又∵AD=BC,
在△ADE和△CBF中.
∠ADE=∠CBF,∠AED=∠CFB,AD=BC,
∴△ADE≌△CBF(AAS).
∴∠AED=∠BFC,∠EAD=∠FCB.
又∵∠DAB=∠BCD,
∴∠EAF=∠FCE.
∴四边形EAFC是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,不正确的是( )
A.在同一平面内,过一点有而且只有一条直线与已知直线垂直
B.经过直线外一点,有而且只有一条直线与这条直线平行
C.垂直于同一直线的两条直线垂直
D.平行于同一直线的两条直线平行 -
科目: 来源: 题型:
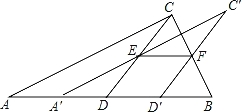
查看答案和解析>>【题目】(2016湖南省邵阳市第10题)如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】果品店刚试营业,就在批发市场购买某种水果销售,第一次用500元购进若干千克水果,并以每千克定价7元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了20%,用660元所购买的数量比第一次多10千克.仍以原来的单价卖完.
求第一次该种水果的进价是每千克多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出下列已知点关于原点对称点的坐标.
A(-2,3) B(5,-5) C(-3,-7) D(3,-2) E(4,6) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是
A. 直线一定比射线长 B. 角的两边越长,角度就越大
C. a一定是正数,-a一定是负数 D. -1是最大的负整数
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适宜采用全面调查的是( )
A. 了解我省中学生的视力情况 B. 了解九(1)班学生校服的尺码情况
C. 检测一批电灯泡的使用寿命 D. 调查《体育新闻》栏目的收视率
相关试题

