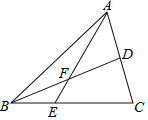
【题目】如图,△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,则EF:AF=_____;若S△ABC=12,则S△ADF﹣S△BEF=_____.
参考答案:
【答案】![]() 2
2
【解析】
过D作DG∥AE交CE于G,由点D是AC的中点,得到AD=![]() AC,CG=EG,进而求得EF=
AC,CG=EG,进而求得EF=![]() DG,AF=
DG,AF=![]() DG,从而得到EF与AF的比,然后分别求出S△ABD,S△ABE再根据S△ADF﹣S△BEF=S△ABD﹣S△ABE即可求出最后的结果.
DG,从而得到EF与AF的比,然后分别求出S△ABD,S△ABE再根据S△ADF﹣S△BEF=S△ABD﹣S△ABE即可求出最后的结果.
过D作DG∥AE交CE于G,
∵点D是AC的中点,
∴AD=![]() AC,CG=EG,
AC,CG=EG,
∴AE=2DG,CE=2CG,
∵EC=2BE,
∴BE=EG,
∴EF=![]() DG,
DG,
∴AF=![]() DG,
DG,
∴EF:AF=![]() ,
,
∵S△ABC=12,
∴S△ABD=![]() S△ABC=
S△ABC=![]() ×12=6.
×12=6.
∵EC=2BE,S△ABC=12,
∴S△ABE=![]() S△ABC=
S△ABC=![]() ×12=4,
×12=4,
∵S△ABD﹣S△ABE=(S△ADF+S△ABF)﹣(S△ABF+S△BEF)=S△ADF﹣S△BEF,
即S△ADF﹣S△BEF=S△ABD﹣S△ABE=6﹣4=2.
故答案为:![]() ,2.
,2.
-
科目: 来源: 题型:
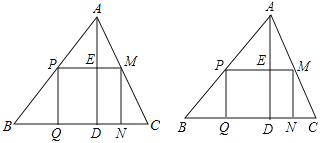
查看答案和解析>>【题目】如图:有一块余料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm.
(1)如果把它加工成长方形零件,使长方形的一边在BC上,其余两个顶点分别在AB、AC上,设长方形宽xmm,面积为ymm2,那么宽为多少时,其面积最大.最大面积是多少?
(2)若以BC的中点O为原点建立平面直角坐标系,B(-60,0),AD=BD.
求过A、B、C三点的抛物线解析式;
在此抛物线对称轴上是否存在一点R,使以A、B、R为顶点的三角形是直角三角形.若存在,请直接写出R点的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度. 小军为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.
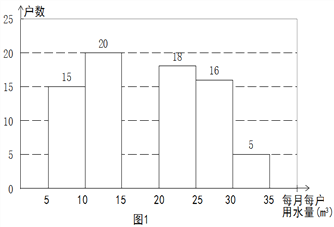
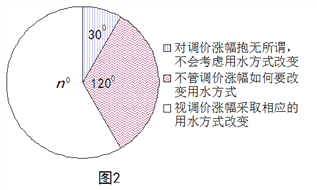
小军发现每月每户的用水量在5m3-35m3之间,有7户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变. 根据小军绘制的图表和发现的信息,完成下列问题:
(1)n =________,小明调查了_____户居民,并补全图1;
(2)每月每户用水量的中位数落在______之间,众数落在_______之间;
(3)如果小明所在的小区有1200户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元.在同时购进两种不同型号电视机的方案中,为使销售利润最多,你选择哪一种进货方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,BD=DC,∠ABD=∠ACD,求证:AD平分∠BAC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 与
与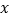 轴交于A、B两点,点P在函数
轴交于A、B两点,点P在函数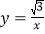 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).A. 2个 B. 3个 C. 4个 D. 6个
相关试题

