【题目】抛物线![]() 与
与![]() 轴交于A、B两点,点P在函数
轴交于A、B两点,点P在函数![]() 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
A. 2个 B. 3个 C. 4个 D. 6个
参考答案:
【答案】D
【解析】分析:先由二次函数与一元二次方程的关系求出A、B两点的坐标,然后分类讨论:①当∠PAB=90°时,则P点的横坐标为-3,根据反比例函数图象上点的坐标特征易得P点有1个;②当∠APB=90°,设P(x,![]() ),根据两点间的距离公式和勾股定理可得(x+3)2+(
),根据两点间的距离公式和勾股定理可得(x+3)2+(![]() )2+(x-3)2+(
)2+(x-3)2+(![]() )2=36,此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,此时P点有1个.
)2=36,此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,此时P点有1个.
详解:解![]() 得,
得,
x=±3,
∴A(-3,0),B(3,0).
①当∠PAB=90°时,如图1,P点的横坐标为-3,把x=-3代入y=![]() 得y=-
得y=-![]() ,所以此时P点有1个;
,所以此时P点有1个;
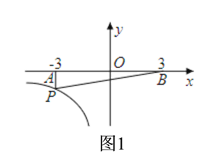
②当∠APB=90°,如图2,设P(x,![]() ),PA2=(x+3)2+(
),PA2=(x+3)2+(![]() )2,PB2=(x-3)2+(
)2,PB2=(x-3)2+(![]() )2,AB2=(3+3)2=36,
)2,AB2=(3+3)2=36,
∵PA2+PB2=AB2,
∴(x+3)2+(![]() )2+(x-3)2+(
)2+(x-3)2+(![]() )2=36,
)2=36,
整理得x4-9x2+4=0,所以x2=![]() ,或x2=
,或x2=![]() ,
,
所以此时P点有4个,
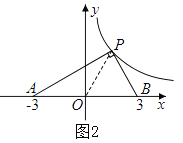
③当∠PBA=90°时,如图3,P点的横坐标为3,把x=3代入y=![]() 得y=
得y=![]() ,所以此时P点有1个;
,所以此时P点有1个;
综上所述,满足条件的P点有6个.
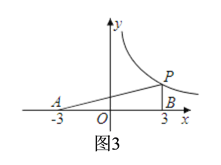
故选:D.
-
科目: 来源: 题型:
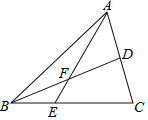
查看答案和解析>>【题目】如图,△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,则EF:AF=_____;若S△ABC=12,则S△ADF﹣S△BEF=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,BD=DC,∠ABD=∠ACD,求证:AD平分∠BAC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(直接写结果)
(1)- 5+ 2 =
(2)-5-2=
(3)5-(-2)=
(4)(-5)×(-2)=
(5)(-2)÷(-6)=
(6)
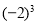 =
=(7)
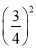 =
= (8)
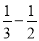 =
= (9)
 =
= (10)
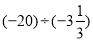 =
= -
科目: 来源: 题型:
查看答案和解析>>【题目】2013年4月20日,四川省雅安市芦山县发生了7.0级地震,某校开展了“雅安,我们在一起”的赈灾捐款活动,其中九年级二班50名学生的捐款情况如下表所示:
捐款金额(元)
5
10
15
20
50
捐款人数(人)
7
18
10
12
3
(1)求这50个样本数据的平均数、众数和中位数;
(2)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划购买A、B两种计算器共100个,要求A种计算器数量不低于B种的
 ,且不高于B种的
,且不高于B种的 .已知A、B两种计算器的单价分别是150元/个、100元/个,设购买A种计算器x个.
.已知A、B两种计算器的单价分别是150元/个、100元/个,设购买A种计算器x个.(1)求计划购买这两种计算器所需费用y(元)与x的函数关系式;
(2)问该公司按计划购买者两种计算器有多少种方案?
(3)由于市场行情波动,实际购买时,A种计算器单价下调了3m(m>0)元/个,同时B种计算器单价上调了2m元/个,此时购买这两种计算器所需最少费用为12150元,求m的值.
相关试题

