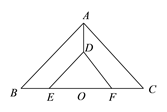
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
参考答案:
【答案】D
【解析】试题分析:∵根据作法可知:MN是线段AD的垂直平分线,∴AE=DE,AF=DF,∴∠EAD=∠EDA,∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠EDA=∠CAD,∴DE∥AC,同理DF∥AE,∴四边形AEDF是菱形,∴AE=DE=DF=AF,∵AF=4,∴AE=DE=DF=AF=4,∵DE∥AC,∴![]() =
=![]() ,∵BD=6,AE=4,CD=3,∴
,∵BD=6,AE=4,CD=3,∴![]() =
=![]() ,∴BE=8,故选D.
,∴BE=8,故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条长为60cm的卷尺铺平后折叠,使得卷尺自身的一部分重合,然后在重合部分(阴影处)沿与卷尺边垂直的方向剪一刀,此时卷尺分为了三段,若这三段长度由短到长的比为1:2:3,则折痕对应的刻度的可能性有 ( )
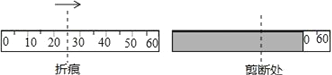
A. 4种 B. 5种 C. 6种 D. 7种
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰
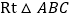 和等腰
和等腰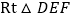 中,斜边
中,斜边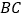 中点
中点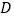 也是
也是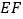 的中点,
的中点,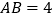 ,
,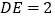 .
.
(
 )如图,则
)如图,则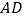 与
与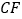 的关系是__________.
的关系是__________.(
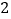 )将
)将 绕点
绕点 顺时针旋转
顺时针旋转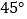 ,请画出图形井求
,请画出图形井求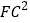 的值.
的值.(
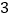 )将
)将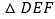 绕点
绕点 逆时针旋转,角度为
逆时针旋转,角度为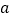 ,请判断(
,请判断(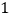 )的结论是否仍然成立,若成立请证明,若不成立请画图说明.
)的结论是否仍然成立,若成立请证明,若不成立请画图说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是几次活动汇总后统计的数据:
摸球的次数s
150
200
500
900
1000
1200
摸到白球的频数n
51
64
156
275
303
361
摸到白球的频率
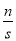
0.34
0.32
0.312
0.306
0303
0.301
(1)请估计:当次数s很大时,摸到白球的频率将会接近 ;假如你去摸一次,你摸到白球的概率是 (精确到0.1).
(2)试估算口袋中红球有多少只?
(3)解决了上面的问题后请你从统计与概率方面谈一条启示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为线段
为线段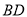 上一动点,分别过点
上一动点,分别过点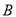 、
、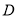 作
作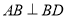 ,
,  ,连接
,连接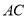 、
、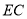 ,已知
,已知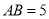 ,
,  ,
, 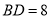 ,设
,设 .
.(1)用含
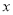 的代数式表示
的代数式表示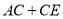 的长;
的长;(2)请问点
 在什么位置时,
在什么位置时, 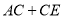 的值最小,求出这个最小值;
的值最小,求出这个最小值;(3)根据(2)中的规律和结论,构图求出代数式
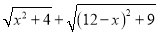 的最小值.
的最小值.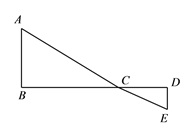
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=
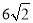 米,背水坡CD的坡度i=1:
米,背水坡CD的坡度i=1: 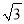 (i为DF与FC的比值),则背水坡CD的坡长为_______米.
(i为DF与FC的比值),则背水坡CD的坡长为_______米.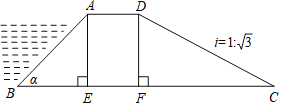
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在四边形ABCD中,∠D=37°,点E是BC边上一点,沿AE折叠,点B落在AD上B′处,若B′E∥CD,则∠B=_________°.

(2)如图2,在四边形ABCD中,AB∥CD,点E是BC边上一点,沿AE折叠,点B落在AD上B′处,点F是BC边上一点,沿DF折叠,点C落在AD上C′处.B′E与C′F有何位置关系?为什么?
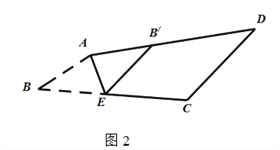
(3)如图3,在四边形ABCD中,∠B=∠D=90°,点E是BC边上一点,沿AE折叠,点B落在AD上B′处,点F是AD边上一点,沿CF折叠,点D落在BC上D′处.试问:AE与CF有何位置关系?说明理由.

(4)在四边形ABCD中,点E是BC边上一点,沿AE折叠.
①若点B落在四边形ABCD内B′处(如图4),则∠1,∠2,∠BAD,∠B之间的数量关系为________.
②若点B落在四边形ABCD外B′处(如图5),则∠1,∠2,∠BAD,∠B之间的数量关系为 ______.

相关试题

