【题目】在等腰![]() 和等腰
和等腰![]() 中,斜边
中,斜边![]() 中点
中点![]() 也是
也是![]() 的中点,
的中点,![]() ,
,![]() .
.
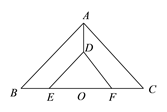
(![]() )如图,则
)如图,则![]() 与
与![]() 的关系是__________.
的关系是__________.
(![]() )将
)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,请画出图形井求
,请画出图形井求![]() 的值.
的值.
(![]() )将
)将![]() 绕点
绕点![]() 逆时针旋转,角度为
逆时针旋转,角度为![]() ,请判断(
,请判断(![]() )的结论是否仍然成立,若成立请证明,若不成立请画图说明.
)的结论是否仍然成立,若成立请证明,若不成立请画图说明.
参考答案:
【答案】(![]() )相等且垂直;(
)相等且垂直;(![]() )
)![]() ;(
;(![]() )见解析
)见解析
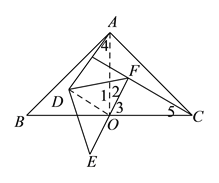
【解析】试题分析:(1)连接AO,A1O,如图1,根据等腰直角三角形的性质得AO⊥OC,AO=OC,A1O⊥OC1,OA1=OC1,则可判断A点、A1点、O点共线,于是得到AA1⊥C1C,AA1=C1C;
(2)先求得FG和GC,再在直角三角形GCF中根据![]() 求值;
求值;
(3)连接OA,DO,如图2,利用旋转的性质得∠AOD=∠COF,则可利用“SAS”证明△OAD≌△OCF,所以AD=FC,∠OAD=∠OCF,再利用三角形内角和得到∠MHC=∠MOA=90°,于是得到AD⊥FC;
试题解析:
(1)连接AO,DO,如图所示:
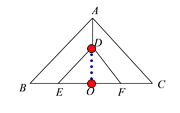
∵△ABC和△DEF都是等腰直角三角形,斜边EF中点O也是BC的中点,
∴AO⊥OC,AO=OC,DO⊥OF,OD=OF,
∴A点、D点、O点共线,
∴AD⊥FC,OA-OD=OC-OD,
∴AD=FC;
(![]() )∵旋转
)∵旋转
∴![]() .
.
∵等腰![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 为等腰
为等腰![]() .
.
在![]() 中
中
![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]()
∴![]() .
.
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]()
∴![]() ,
,
∴![]() .
.
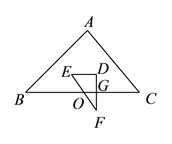
(![]() )连接
)连接![]() 、
、![]() .
.
∵等腰![]() ,
,![]() 为
为![]() 中点
中点
∴![]() ,
,![]()
∴![]() 为等腰
为等腰![]() ,
,
∴![]() .
.
∵等腰![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,
,![]() ,
,
∴![]() 为等腰
为等腰![]() ,
,
∴![]() .
.
∵![]()
∴![]() .
.
在![]() 和
和![]() 中
中
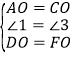 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() .
.
∵![]()
∴![]()
∴![]() ,
,
∴(![]() )则结论仍成立.
)则结论仍成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小丽做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
63
124
178
302
481
599
1803
摸到白球的频率

0.63
0.62
0.593
0.604
0.601
0.599
0.601
(1)请估计:当实验次数为10000次时,摸到白球的频率将会接近 ;(精确到0.1)
(2)假如由你摸球一次,你摸到白球的概率P(摸到白球)= ;
(3)盒子中有黑球 个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中,①∠A+∠B=∠C; ②∠A:∠B:∠C=1:2:3; ③∠A=
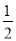 ∠B=
∠B=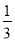 ∠C;
∠C;④∠A=∠B=2∠C; ⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条长为60cm的卷尺铺平后折叠,使得卷尺自身的一部分重合,然后在重合部分(阴影处)沿与卷尺边垂直的方向剪一刀,此时卷尺分为了三段,若这三段长度由短到长的比为1:2:3,则折痕对应的刻度的可能性有 ( )
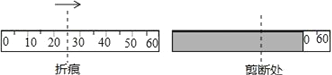
A. 4种 B. 5种 C. 6种 D. 7种
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是几次活动汇总后统计的数据:
摸球的次数s
150
200
500
900
1000
1200
摸到白球的频数n
51
64
156
275
303
361
摸到白球的频率
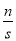
0.34
0.32
0.312
0.306
0303
0.301
(1)请估计:当次数s很大时,摸到白球的频率将会接近 ;假如你去摸一次,你摸到白球的概率是 (精确到0.1).
(2)试估算口袋中红球有多少只?
(3)解决了上面的问题后请你从统计与概率方面谈一条启示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于
 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
A. 2 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为线段
为线段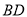 上一动点,分别过点
上一动点,分别过点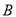 、
、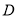 作
作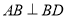 ,
,  ,连接
,连接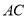 、
、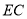 ,已知
,已知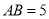 ,
,  ,
, 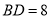 ,设
,设 .
.(1)用含
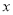 的代数式表示
的代数式表示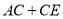 的长;
的长;(2)请问点
 在什么位置时,
在什么位置时, 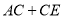 的值最小,求出这个最小值;
的值最小,求出这个最小值;(3)根据(2)中的规律和结论,构图求出代数式
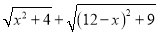 的最小值.
的最小值.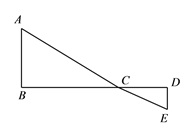
相关试题

