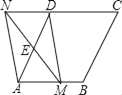
【题目】如图,在菱形ABCD中,AB=4,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)当AM的值为 时,四边形AMDN是矩形,请你把猜想出的AM值作为已知条件,说明四边形AMDN是矩形的理由.
参考答案:
【答案】(1)见解析(2)当AM=2时,说明四边形是矩形
【解析】
(1)根据菱形的性质可得AB∥CD,根据两直线平行,内错角相等可得∠NDE=∠MAE,根据对顶角相等可得∠DEN=∠AEM,根据中点的定义求出DE=AE,然后利用“角边角”证明△NDE和△MAE全等,根据全等三角形对应边相等得到ND=AM,然后利用一组对边平行且相等的四边形是平行四边形证明;
(2)首先证明△AEM是等边三角形,进而得到AE=ED=EM,利用三角形一边上的中线等于斜边一半判断出△AMD是直角三角形,进而得出四边形AMDN是矩形.
(1)∵点E是AD边的中点,
∴AE=ED,
∵AB∥CD,
∴∠NDE=∠MAE,
在△NDE和△MAE中,
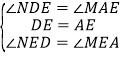 ,
,
∴△NDE≌△MAE(ASA),
∴ND=AM,
∵ND∥AM,
∴四边形AMDN是平行四边形;
(2)当AM=2时,说明四边形是矩形.
∵E是AD的中点,
∴AE=2,
∵AE=AM,∠EAM=60°,
∴△AME是等边三角形,
∴AE=EM,
∴AE=ED=EM,
∴∠AMD=90°,
∵四边形ABCD是菱形,
故当AM=2时,四边形AMDN是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在菱形ABCD中,AC是对角线,CD=CE,连接DE.
(1)若AC=16,CD=10,求DE的长.
(2)G是BC上一点,若GC=GF=CH且CH⊥GF,垂足为P,求证:
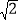 DH=CF.
DH=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,
(1)若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;
(2)若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+2ax+c的图象与x轴交于A、B两点(点A在点B的左边)AB=4,与y轴交于点C,OC=OA,点D为抛物线的顶点.
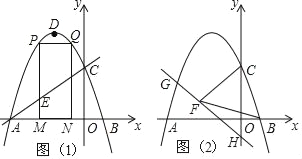
(1)求抛物线的解析式;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM,如图1,点P在点Q左边,当矩形PQNM的周长最大时,求m的值,并求出此时的△AEM的面积;
(3)已知H(0,﹣1),点G在抛物线上,连HG,直线HG⊥CF,垂足为F,若BF=BC,求点G的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,∠DOC=2∠ACD=90°.
(1)求证:直线AC是圆O的切线;
(2)如果∠ACB=75°,圆O的半径为2,求BD的长.

-
科目: 来源: 题型:
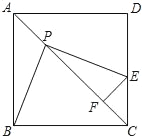
查看答案和解析>>【题目】已知边长为1的正方形ABCD中, P是对角线AC上的一个动点(与点A、C不重合),过点P作PE⊥PB ,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F.
(1)当点E落在线段CD上时(如图),
①求证:PB=PE;
②在点P的运动过程中,PF的长度是否发生变化?若不变,试求出这个不变的值,若变化,试说明理由;
(2)当点E落在线段DC的延长线上时,在备用图上画出符合要求的大致图形,并判断上述(1)中的结论是否仍然成立(只需写出结论,不需要证明);
(3)在点P的运动过程中,△PEC能否为等腰三角形?如果能,试求出AP的长,如果不能,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是弧
 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是 
A. (sinα,sinα) B. (cosα,cosα) C. (cosα,sinα) D. (sinα,cosα)
相关试题

