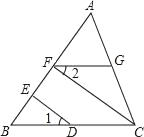
【题目】如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证:FG∥BC.
证明:∵CF⊥AB、DE⊥AB(已知)
∴∠BED=90°、∠BFC=90°
∴∠BED=∠BFC
∴( )∥( )( )
∴∠1=∠BCF( )
又∵∠1=∠2(已知)
∴∠2=∠BCF( )
∴FG∥BC( )
参考答案:
【答案】见解析.
【解析】
根据垂直定义求出∠BED=∠BFC,根据平行线的判定得出ED∥FC,根据平行线的性质得出∠1=∠BCF,求出∠2=∠BCF,根据平行线的判定推出即可.
∵CF⊥AB、DE⊥AB(已知)
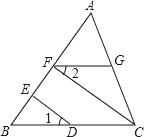
∴∠BED=90°、∠BFC=90°
∴∠BED=∠BFC
∴DE∥CF(同位角相等,两直线平行),
∴∠1=∠BCF(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∴∠2=∠BCF(等量代换),
∴FG∥BC(内错角相等,两直线平行 ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 ,直线
,直线 和直线
和直线 、
、 交于点
交于点 和
和 ,点
,点 是直线
是直线 上一动点.
上一动点.


图1 图2 图3
(1)如图1,当点
 在线段
在线段 上运动时,
上运动时, ,
, ,
, 之间存在什么数量关系?请你猜想结论并说明理由
之间存在什么数量关系?请你猜想结论并说明理由(2)当点
 在
在 、
、 两点的外侧运动时(
两点的外侧运动时( 点与点
点与点 、
、 不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出
不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出 ,
, ,
, 之间的数量关系,不必写理由.
之间的数量关系,不必写理由. -
科目: 来源: 题型:
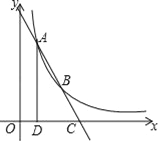
查看答案和解析>>【题目】如图,点A(1,4)、B(2,a)在函数y=
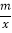 (x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
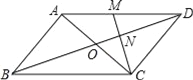
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①DE=CD;②AD平分∠CDE;③∠BAC=∠BDE;④BE+AC=AB,其中正确的是( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
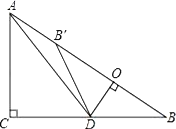
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )

A.2B.2.5或3.5
C.3.5或4.5D.2或3.5或4.5
相关试题

