【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①DE=CD;②AD平分∠CDE;③∠BAC=∠BDE;④BE+AC=AB,其中正确的是( )

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】
①根据角平分线的性质得出结论:DE=CD;
②证明△ACD≌△AED,得AD平分∠CDE;
③由四边形的内角和为360°得∠CDE+∠BAC=180°,再由平角的定义可得结论是正确的;
④由△ACD≌△AED得AC=AE,再由AB=AE+BE,得出结论是正确的.
①∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴DE=CD;
所以此选项结论正确;
②∵DE=CD,AD=AD,∠ACD=∠AED=90°,
∴△ACD≌△AED,
∴∠ADC=∠ADE,
∴AD平分∠CDE,
所以此选项结论正确;
③∵∠ACD=∠AED=90°,
∴∠CDE+∠BAC=360°-90°-90°=180°,
∵∠BDE+∠CDE=180°,
∴∠BAC=∠BDE,
所以此选项结论正确;
④∵△ACD≌△AED,
∴AC=AE,
∵AB=AE+BE,
∴BE+AC=AB,
所以此选项结论正确;
本题正确的结论有4个,故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,从边长为a的正方形纸片中减去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形(其面积=
 ).
).(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a、b的式子表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:在△ABC中,AB、BC、AC三边的长分别为
 、
、 、
、 ,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.(1)请你将△ABC的面积直接填写在横线上: .
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别
 a、
a、 a、
a、 a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索研究:已知:△ABC和△CDE都是等边三角形.
(1)如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为: ,线段AD与BE所成的锐角度数为 °;
(2)如图2,当点A、C、E不在一条直线上时,请证明(1)中的结论仍然成立;
灵活运用:
如图3,某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,试求水池两旁B、D两点之间的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是



A. 55° B. 60° C. 65° D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列命题中:①过一点有且只有一条直线与已知直线平行;②平方根与立方根相等的数有
 和
和 ;③在同一平面内,如果
;③在同一平面内,如果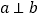 ,
, ,则
,则 ;④直线
;④直线 外一点
外一点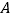 与直线
与直线 上各点连接而成的所有线段中,最短线段的长是
上各点连接而成的所有线段中,最短线段的长是 ,则点
,则点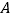 到直线
到直线 的距离是
的距离是 ;⑤无理数包括正无理数、零和负无理数.其中真命题的个数是( )
;⑤无理数包括正无理数、零和负无理数.其中真命题的个数是( )A.
 个B.
个B.  个C.
个C.  个D.
个D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线
 经过第一象限内一点A,且OA=4过点A作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,则点C的坐标为( )
经过第一象限内一点A,且OA=4过点A作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,则点C的坐标为( )
A. (
 ,2) B. (
,2) B. ( ,1)
,1)C. (-2,
 ) D. (-1,
) D. (-1, )
)
相关试题

