【题目】已知直线![]() ,直线
,直线![]() 和直线
和直线![]() 、
、![]() 交于点
交于点![]() 和
和![]() ,点
,点![]() 是直线
是直线![]() 上一动点.
上一动点.



图1 图2 图3
(1)如图1,当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() ,
,![]() ,
,![]() 之间存在什么数量关系?请你猜想结论并说明理由
之间存在什么数量关系?请你猜想结论并说明理由
(2)当点![]() 在
在![]() 、
、![]() 两点的外侧运动时(
两点的外侧运动时(![]() 点与点
点与点![]() 、
、![]() 不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出
不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出![]() ,
,![]() ,
,![]() 之间的数量关系,不必写理由.
之间的数量关系,不必写理由.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)过点P作PE∥l1,根据平行线的性质即可得到,∠APE=∠PAC,∠BPE=∠PBD,根据∠APE+∠BPE=∠PAC+∠PBD,可得∠APB=∠PAC+∠PBD;
(2)根据(1)的方法,过点P作PE∥l1,根据平行线的性质,可得∠APE=∠PAC,∠PBD=∠BPE,图2中根据∠APB=∠APE-∠BPE,可得∠PAC=∠APB+∠PBD;图3中,根据∠APB=∠BPE-∠APE,可得∠PBD=∠PAC+∠APB.
解:(1)∠APB=∠PAC+∠PBD,
如图1,过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∴∠APE+∠BPE=∠PAC+∠PBD,
∴∠APB=∠PAC+∠PBD;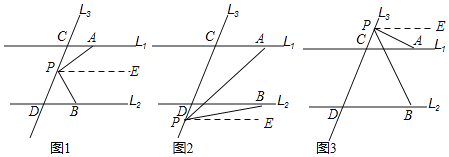
(2)不成立,
如图2:∠PAC=∠APB+∠PBD,
理由:过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵∠APB=∠APE-∠BPE=∠PAC-∠PBD,
∴∠PAC=∠APB+∠PBD;
如图3:∠PBD=∠PAC+∠APB,
理由:过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵APB=∠BPE-∠APE=∠PBD-∠PAC,
∴∠PBD=∠PAC+∠APB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD是边AB上的高,且
 .
.(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备开展“阳光体有活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
各项目人数条形统计图 各项目人数扇形统计图


(1)这次活动一共调查了______名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择乒乓球项目的人数所在扇形的圆心角等于_____度;
(4)若该学校有
 人,请你估计该学校选择足球项目的学生人数约是多少人.?
人,请你估计该学校选择足球项目的学生人数约是多少人.? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(1,4)、B(2,a)在函数y=
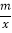 (x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
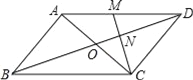
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
-
科目: 来源: 题型:
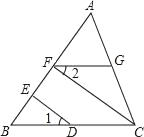
查看答案和解析>>【题目】如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证:FG∥BC.
证明:∵CF⊥AB、DE⊥AB(已知)
∴∠BED=90°、∠BFC=90°
∴∠BED=∠BFC
∴( )∥( )( )
∴∠1=∠BCF( )
又∵∠1=∠2(已知)
∴∠2=∠BCF( )
∴FG∥BC( )
相关试题

