【题目】如图,等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点.线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t.则大致反映S与t变化关系的图象是( )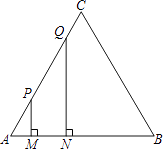
A.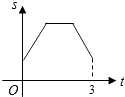
B.
C.
D.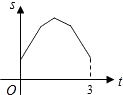
参考答案:
【答案】A
【解析】解:过点C作CG⊥AB,

∵MN=1,四边形MNQP为直角梯形,
∴四边形MNQP的面积为S= ![]() MN×(PM+QN),
MN×(PM+QN),
∴N点从A到G点四边形MNQP的面积为S= ![]() MN×(PM+QN)中,PM,QN都在增大,所以面积也增大;
MN×(PM+QN)中,PM,QN都在增大,所以面积也增大;
当QN=CG时,QN开始减小,但PM仍然增大,且PM+QN不变,
∴四边形MNQP的面积不发生变化,
当PM<CG时,PM+QN开始减小,
∴四边形MNQP的面积减小,
∴符合要求的只有A.
所以答案是:A.
【考点精析】掌握直角梯形是解答本题的根本,需要知道一腰垂直于底的梯形是直角梯形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).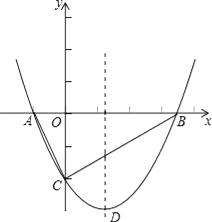
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】直线l:y=mx﹣m+1(m为常数,且m≠0)与坐标轴交于A、B两点,若△AOB(O是原点)的面积恰为2,则符合要求的直线l有( )
A.1条
B.2条
C.3条
D.4条 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,G是线段AB上一点,AC和DG相交于点E.
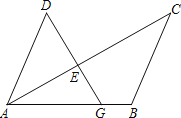
(1)请先作出∠ABC的平分线BF,交AC于点F;(尺规作图,保留作图痕迹,不写作法与证明)
(2)然后证明当:AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,AC上的中线BD把三角形的周长分为24㎝和30㎝的两个部分,求三角形的三边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个运输队承包了一家公司运送货物的业务,第一次运送18吨,派了1辆大卡车和5辆小卡车;第二次运送38吨,派了2辆大卡车和11辆小卡车,并且两次派的车都刚好装满。
(1)两种车型的载重量各是多少吨?
(2)若大卡车运送一次的费用为200元,小卡车运送一次的费用为60元,在第一次运送过程中怎样安排大小车辆,才能使费用最少?(直接写出派车方案)
-
科目: 来源: 题型:
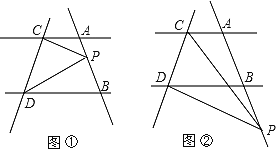
查看答案和解析>>【题目】如图,已知直线AC∥BD,直线AB、CD不平行,点P在直线AB上,且和点A、B不重合.
(1)如图①,当点P在线段AB上时,若∠PCA=20°,∠PDB=30°,求∠CPD的度数;
(2)点P在A、B两点之间运动时,∠PCA、∠PDB、∠CPD之间满足什么样的等量关系(直接写出答案);
(3)如图②,当点P在线段AB的延长线上运动时,∠PCA、∠PDB、∠CPD之间满足什么样的等量关系,并说明理由。
相关试题

