【题目】已知直线L:y=3x+2,现有下列命题:
①过点P(-1,1)与直线L平行的直线是y=3x+4;②若直线L与x轴、y轴分别交于A、B两点,则AB=![]() ;③若点M(-
;③若点M(-![]() ,1),N(a,b)都在直线L上,且a>-
,1),N(a,b)都在直线L上,且a>-![]() ,则b>1; ④若点Q到两坐标轴的距离相等,且Q在L上,则点Q在第一或第二象限。其中正确的命题是_________.
,则b>1; ④若点Q到两坐标轴的距离相等,且Q在L上,则点Q在第一或第二象限。其中正确的命题是_________.
参考答案:
【答案】①②③.
【解析】
由于k相等,只需判断点P是否在直线y=3x+4上即可判断①;先确定点A、B的坐标,再根据勾股定理可求得AB的长,即可判断②;根据一次函数的增减性可对③进行判断;解y=3x+4与y=x或y=-x所组成的方程组,可求得Q点的坐标,即可对④进行判断.
解:当x=-1时,y=3×(-1)+4=1,所以过点P(-1,1)与直线L平行的直线是y=3x+4,所以①正确;
对于直线L:y=3x+2,当![]() 时,
时,![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() ,所以A点坐标为(
,所以A点坐标为(![]() ,0),B点坐标为(0,2),所以AB=
,0),B点坐标为(0,2),所以AB=![]() ,所以②正确;
,所以②正确;
对于y=3x+2,∵k=3>0,∴y随x的增大而增大,所以当![]() 时,b>1,所以③正确;
时,b>1,所以③正确;
解方程组![]() ,得
,得![]() ,解方程组
,解方程组![]() ,得
,得 ,即Q点的坐标为(-1,-1)或(
,即Q点的坐标为(-1,-1)或(![]() ),所以④错误.
),所以④错误.
故答案为①②③.
-
科目: 来源: 题型:
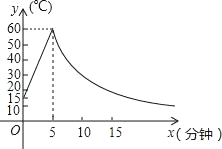
查看答案和解析>>【题目】如图为某种材料温度y(℃)随时间x(min)变化的函数图象.已知该材料初始温度为15℃,温度上升阶段y与时间x成一次函数关系,且在第5分钟温度达到最大值60℃后开始下降;温度下降阶段,温度y与时间x成反比例关系.
(1)分别求该材料温度上升和下降阶段,y与x间的函数关系式;
(2)根据工艺要求,当材料的温度高于30℃时,可以进行产品加工,问可加工多长时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按下图的方式搭塔式三角形,第一个图用了3根火柴棒,第二个图用了9根火柴棒,第三个图用了18根火柴棒,......,照这样下去,第9个图用了_____根火柴棒.
 ……
…… -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
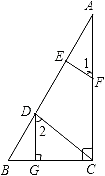
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠ (等量代换)
∴EF∥CD( )
∴∠AEF=∠ ( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°( )
∴CD⊥AB( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下列材料.
“分数均可化为有限小数或无限循环小数”,反之,“有限小数或无限小数均可化为分数”.
例如:
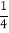 =1÷4=0.25;
=1÷4=0.25;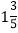 =
=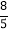 =8÷5=1.6;
=8÷5=1.6; =1÷3=
=1÷3= ,反之,0.25=
,反之,0.25=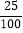 =
=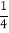 ;1.6=
;1.6=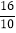 =
=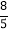 =
=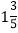 .那么
.那么 ,
,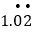 怎么化成分数呢?
怎么化成分数呢?解:∵
 ×10=3+
×10=3+ , ∴不妨设
, ∴不妨设 =x,则上式变为10x=3+x,解得x=
=x,则上式变为10x=3+x,解得x= ,即
,即 =
= ;
;∵
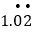 =
=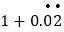 ,设
,设 =x,则上式变为100x=2+x,解得x=
=x,则上式变为100x=2+x,解得x=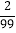 ,
,∴
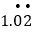 =
=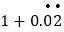 =1+x=1+
=1+x=1+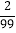 =
=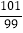
⑴将分数化为小数:
 =______,
=______,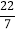 =_______;
=_______;⑵将小数化为分数:
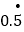 =______,
=______,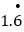 =_______;
=_______;⑶将小数
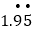 化为分数,需要写出推理过程.
化为分数,需要写出推理过程. -
科目: 来源: 题型:
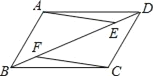
查看答案和解析>>【题目】如图,在ABCD中,点E、F在BD上,且BF=DE.
(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形.
-
科目: 来源: 题型:
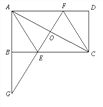
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点O是AC中点,AC=2AB,延长AB到G,使BG=AB,连接GO并延长,分别交BC于点E,交AD于点F.
(1)求证:△ABC≌△AOG;
(2)若ABCD为矩形,则四边形AECF是什么特殊四边形?请说明理由.
相关试题

