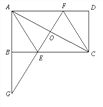
【题目】如图,在平行四边形ABCD中,点O是AC中点,AC=2AB,延长AB到G,使BG=AB,连接GO并延长,分别交BC于点E,交AD于点F.
(1)求证:△ABC≌△AOG;
(2)若ABCD为矩形,则四边形AECF是什么特殊四边形?请说明理由.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】(1)由O是AC的中点,AC=2AB,BG=AB,得到AO=AB,AC=AG.由∠BAC=∠OAG ,即可得到结论;
(2)由O是AC的中点,得到AO=OC.由平行四边形的性质得到AF∥EC,由平行线的性质得到∠DAO=∠BCO,进而得到△AOF≌△COE, AF=CE,得到四边形AECF是平行四边形.由△ABC≌△AOG,得到∠AOG=∠ABC=90°,即可得到AECF是菱形.
(1)∵O是AC的中点,AC=2AB,BG=AB,∴AO=AB,AC=AG.
又∵∠BAC=∠OAG ,∴△ABC≌△AOG;
(2)AECF是菱形.理由如下:
∵O是AC的中点,∴AO=OC.
∵平行四边形ABCD,∴AF∥EC,∴∠DAO=∠BCO.
又∵∠AOF=∠COE,∴△AOF≌△COE,∴AF=CE,∴四边形AECF是平行四边形.
由(1)知△ABC≌△AOG,∴∠AOG=∠ABC.
又∵ABCD是矩形,
∴∠ABC=90°,∴∠AOG=90°,∴AECF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线L:y=3x+2,现有下列命题:
①过点P(-1,1)与直线L平行的直线是y=3x+4;②若直线L与x轴、y轴分别交于A、B两点,则AB=
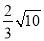 ;③若点M(-
;③若点M(-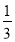 ,1),N(a,b)都在直线L上,且a>-
,1),N(a,b)都在直线L上,且a>-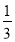 ,则b>1; ④若点Q到两坐标轴的距离相等,且Q在L上,则点Q在第一或第二象限。其中正确的命题是_________.
,则b>1; ④若点Q到两坐标轴的距离相等,且Q在L上,则点Q在第一或第二象限。其中正确的命题是_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下列材料.
“分数均可化为有限小数或无限循环小数”,反之,“有限小数或无限小数均可化为分数”.
例如:
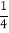 =1÷4=0.25;
=1÷4=0.25;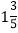 =
=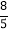 =8÷5=1.6;
=8÷5=1.6; =1÷3=
=1÷3= ,反之,0.25=
,反之,0.25=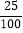 =
=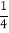 ;1.6=
;1.6=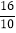 =
=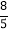 =
=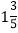 .那么
.那么 ,
,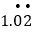 怎么化成分数呢?
怎么化成分数呢?解:∵
 ×10=3+
×10=3+ , ∴不妨设
, ∴不妨设 =x,则上式变为10x=3+x,解得x=
=x,则上式变为10x=3+x,解得x= ,即
,即 =
= ;
;∵
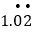 =
=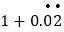 ,设
,设 =x,则上式变为100x=2+x,解得x=
=x,则上式变为100x=2+x,解得x=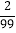 ,
,∴
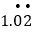 =
=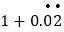 =1+x=1+
=1+x=1+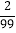 =
=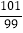
⑴将分数化为小数:
 =______,
=______,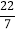 =_______;
=_______;⑵将小数化为分数:
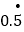 =______,
=______,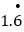 =_______;
=_______;⑶将小数
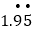 化为分数,需要写出推理过程.
化为分数,需要写出推理过程. -
科目: 来源: 题型:
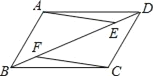
查看答案和解析>>【题目】如图,在ABCD中,点E、F在BD上,且BF=DE.
(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的
距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数
关系
 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出:某段楼梯共有10个台阶,如果某同学在上台阶时,可以一步1个台阶,也可以一步2个台阶.那么该同学从该段楼梯底部上到顶部共有多少种不同的走法?
问题探究:
为解决上述实际问题,我们先建立如下数学模型:
如图①,用若干个边长都为1的正方形(记为1×1矩形)和若干个边长分别为1和2的矩形(记为1×2矩形),要拼成一个如图②中边长分别为1和n的矩形(记为1×
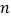 矩形),有多少种不同的拼法?(设
矩形),有多少种不同的拼法?(设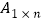 表示不同拼法的个数)
表示不同拼法的个数)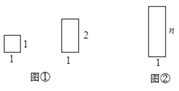
为解决上述数学模型问题,我们采取的策略和方法是:一般问题特殊化.
探究一:先从最特殊的情形入手,即要拼成一个1×1矩形,有多少种不同拼法?
显然,只有1种拼法,如图③,即
 =1种.
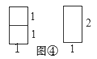
=1种.探究二:要拼成一个1×2矩形,有多少种不同拼法?
可以看出,有2种拼法,如图④,即
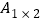 =2种.
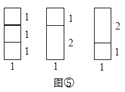
=2种. 探究三:要拼成一个1×3矩形,有多少种不同拼法?
拼图方法可分为两类:一类是在图④这2种1×2矩形上方,各拼上一个1×1矩形,即这类拼法共有
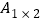 =2种;另一类是在图③这1种1×1矩形上方拼上一个1×2矩形,即这类拼法有
=2种;另一类是在图③这1种1×1矩形上方拼上一个1×2矩形,即这类拼法有 =1种.如图⑤,即
=1种.如图⑤,即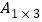 =
=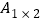 +
+ = 2+1=3(种).
= 2+1=3(种).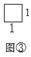
探究四:仿照上述探究过程,要拼成一个1×4矩形,有多少种不同拼法?请画示意图说明并求出结果.
探究五:要拼成一个1×5矩形,仿照上述探究过程,得出
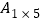 = 种不同拼法.
= 种不同拼法.(直接写出结果,不需画图).
问题解决:请你根据上述中的数学模型,解答“问题提出”中的实际问题.
(写出解答过程,不需画图).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=α°,∠COD在∠AOB内部且∠COD=β°.
(1)若α,β满足|α-2β|+(β-60)2=0,则①α= ;
②试通过计算说明∠AOD与∠COB有何特殊关系;
(2)在(1)的条件下,如果作OE平分∠BOC,请求出∠AOC与∠DOE的数量关系;
(3)若α°,β°互补,作∠AOC,∠DOB的平分线OM,ON,试判断OM与ON的位置关系,并说明理由.

相关试题

