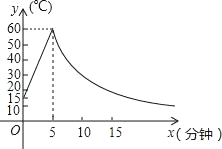
【题目】如图为某种材料温度y(℃)随时间x(min)变化的函数图象.已知该材料初始温度为15℃,温度上升阶段y与时间x成一次函数关系,且在第5分钟温度达到最大值60℃后开始下降;温度下降阶段,温度y与时间x成反比例关系.
(1)分别求该材料温度上升和下降阶段,y与x间的函数关系式;
(2)根据工艺要求,当材料的温度高于30℃时,可以进行产品加工,问可加工多长时间?
参考答案:
【答案】(1) ![]() ,y=
,y=![]() ; (2)
; (2)![]() min.
min.
【解析】
(1)确定两个函数后,找到函数图象经过的点的坐标,用待定系数法求得函数的解析式即可;
(2)分别令两个函数的函数值为30,解得两个x的值相减即可得到答案.
(1)设温度上升阶段一次函数表达式为y=kx+b(k≠0).
∵该函数图象经过点(0,15),(5,60),∴![]() ,解得:
,解得:![]() ,∴一次函数的表达式为y=9x+15(0≤x≤5).
,∴一次函数的表达式为y=9x+15(0≤x≤5).
设温度下降阶段反比例函数表达式为y=![]() (a≠0).
(a≠0).
∵该函数图象经过点(5,60),∴![]() =60,解得:a=300,∴反比例函数表达式为y=
=60,解得:a=300,∴反比例函数表达式为y=![]() (x≥5);
(x≥5);
(2)∵y=9x+15,∴当y=30时,9x+15=30,解得:x=![]() .
.
∵y=![]() ,∴当y=30时,
,∴当y=30时,![]() =30,解得:x=10,10﹣
=30,解得:x=10,10﹣![]() =
=![]() ,所以可加工的时间为
,所以可加工的时间为![]() 分钟.
分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,将△ABD沿AB向下平移使A点到达B点,得到△BEC,下列说法正确的是( )
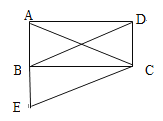
A. △ACE一定是等腰三角形B. △ACE一定是等边三角形
C. △ACE一定是锐角三角形D. △ACE不可能是等腰直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,李强在教学楼的点P处观察对面的办公大楼,为了求得对面办公大楼的高度,李强测得办公大楼顶部点A的仰角为30°,测得办公大楼底部点B的俯角为37°,已知测量点P到对面办公大楼上部AD的距离PM为30m,办公大楼平台CD=10m.求办公大楼的高度(结果保留整数).(参考数据:sin37°≈
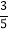 ,tan37°≈
,tan37°≈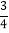 ,
,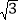 ≈1.73)
≈1.73)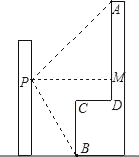
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按下图的方式搭塔式三角形,第一个图用了3根火柴棒,第二个图用了9根火柴棒,第三个图用了18根火柴棒,......,照这样下去,第9个图用了_____根火柴棒.
 ……
…… -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
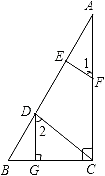
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠ (等量代换)
∴EF∥CD( )
∴∠AEF=∠ ( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°( )
∴CD⊥AB( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线L:y=3x+2,现有下列命题:
①过点P(-1,1)与直线L平行的直线是y=3x+4;②若直线L与x轴、y轴分别交于A、B两点,则AB=
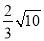 ;③若点M(-
;③若点M(-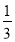 ,1),N(a,b)都在直线L上,且a>-
,1),N(a,b)都在直线L上,且a>-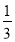 ,则b>1; ④若点Q到两坐标轴的距离相等,且Q在L上,则点Q在第一或第二象限。其中正确的命题是_________.
,则b>1; ④若点Q到两坐标轴的距离相等,且Q在L上,则点Q在第一或第二象限。其中正确的命题是_________.
相关试题

