【题目】在关于x,y的二元一次方程组 ![]() 中.
中.
(1)若a=3.求方程组的解;
(2)若S=a(3x+y),当a为何值时,S有最值.
参考答案:
【答案】
(1)解:当a=3时,方程组为 ![]() ,
,
②×2得,4x﹣2y=2③,
①+③得,5x=5,
解得x=1,
把x=1代入①得,1+2y=3,
解得y=1,
所以,方程组的解是 ![]()
(2)解:方程组的两个方程相加得,3x+y=a+1,
所以,S=a(3x+y)=a(a+1)=(a+ ![]() )2﹣
)2﹣ ![]() ,
,
所以,当a=﹣ ![]() 时,S有最小值﹣
时,S有最小值﹣ ![]()
【解析】(1)用加减消元法求解即可;(2)把方程组的两个方程相加得到3x+y=a+1,然后代入整理,再利用二次函数的最值问题解答.
【考点精析】利用解二元一次方程组和二次函数的最值对题目进行判断即可得到答案,需要熟知二元一次方程组:①代入消元法;②加减消元法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线上有n(n≥2的正整数)个点,每相邻两点间距离为1,从左边第1个点起跳,且同时满足以下三个条件:
①每次跳跃均尽可能最大;
②跳n次后必须回到第1个点;
③这n次跳跃将每个点全部到达,
设跳过的所有路程之和为Sn , 则S25= . -
科目: 来源: 题型:
查看答案和解析>>【题目】体考在即,初三(1)班的课题研究小组对本年级530名学生的体育达标情况进行调查,制作出如图所示的统计图,其中1班有50人.(注:30分以上为达标,满分50分)根据统计图,解答下面问题:
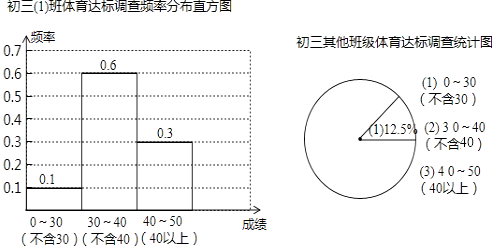
(1)初三(1)班学生体育达标率和本年级其余各班学生体育达标率各是多少?
(2)若除初三(1)班外其余班级学生体育考试成绩在30﹣﹣40分的有120人,请补全扇形统计图;(注:请在图中分数段所对应的圆心角的度数)
(3)如果要求全年级学生的体育达标率不低于90%,试问在本次调查中,该年级全体学生的体育达标率是否符合要求? -
科目: 来源: 题型:
查看答案和解析>>【题目】以图1(以O为圆心,半径1 的半圆)作为“基本图形”,分别经历如下变换能得到图2的序号是 (多填或错填得0分,少填酌情给分)
①只要向右平移1个 单位;
② 先以直线AB为对称轴进行对称变换,再向右平移1个单位;
③先绕着O旋转180°,再向右平移1个单位;
④只要绕着某点旋转180°.

-
科目: 来源: 题型:
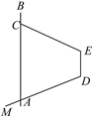
查看答案和解析>>【题目】如图所示,已知射线 DM与直线AB交于点A,线段EC与直线AB交于点C,AB∥DE.
(1)当∠MAC=100°,∠BCE=120°时,把EC绕点E旋转多大角度(所求角度小于180°)时,可判定MD∥EC?请你设计出两种方案,并画出草图;
(2)若将EC绕点E逆时针旋转60°时,点C与点A恰好重合,请画出草图,并在图中找出同位角、内错角各两对(先用数字标出角,再回答).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,P是直线l外一点,点A、B、C在l上,且PB⊥l,下列说法:①PA、PB、PC这3条线段中,PB最短;②点P到直线l的距离是线段PB的长;③线段AB的长是点A到PB的距离;④线段PA的长 是点P到直线l的距离.其中正确的是( )

A.①②③
B.①②④
C.①③④
D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中,AB为直径,点C为圆上一点,将劣弧
 沿弦AC翻折交AB于点D,连结CD.
沿弦AC翻折交AB于点D,连结CD. 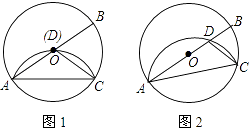
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.
相关试题

