【题目】在⊙O中,AB为直径,点C为圆上一点,将劣弧 ![]() 沿弦AC翻折交AB于点D,连结CD.
沿弦AC翻折交AB于点D,连结CD. 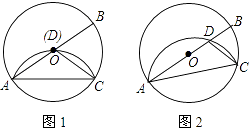
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.
参考答案:
【答案】
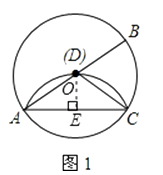
(1)解:如图,过点O作OE⊥AC于E,
则AE= ![]() AC=
AC= ![]() ×2=1,
×2=1,
∵翻折后点D与圆心O重合,
∴OE= ![]() r,
r,
在Rt△AOE中,AO2=AE2+OE2,
即r2=12+( ![]() r)2,
r)2,
解得r= ![]()
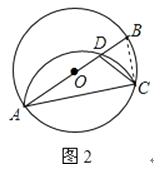
(2)解:连接BC,
∵AB是直径,
∴∠ACB=90°,
∵∠BAC=25°,
∴∠B=90°﹣∠BAC=90°﹣25°=65°,
根据翻折的性质, ![]() 所对的圆周角为∠B,
所对的圆周角为∠B, ![]() 所对的圆周角为∠ADC,
所对的圆周角为∠ADC,
∴∠ADC+∠B=180°,
∴∠B=∠CDB=65°,
∴∠DCA=∠CDB﹣∠A=65°﹣25°=40°.
【解析】(1)过点O作OE⊥AC于E,根据垂径定理可得AE= ![]() AC,再根据翻折的性质可得OE=
AC,再根据翻折的性质可得OE= ![]() r,然后在Rt△AOE中,利用勾股定理列式计算即可得解;(2)连接BC,根据直径所对的圆周角是直角求出∠ACB,根据直角三角形两锐角互余求出∠B,再根据翻折的性质得到
r,然后在Rt△AOE中,利用勾股定理列式计算即可得解;(2)连接BC,根据直径所对的圆周角是直角求出∠ACB,根据直角三角形两锐角互余求出∠B,再根据翻折的性质得到 ![]() 所对的圆周角,然后根据∠ACD等于
所对的圆周角,然后根据∠ACD等于 ![]() 所对的圆周角减去
所对的圆周角减去 ![]() 所对的圆周角,计算即可得解.
所对的圆周角,计算即可得解.
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,以及对垂径定理的理解,了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在关于x,y的二元一次方程组
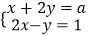 中.
中.
(1)若a=3.求方程组的解;
(2)若S=a(3x+y),当a为何值时,S有最值. -
科目: 来源: 题型:
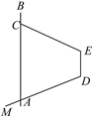
查看答案和解析>>【题目】如图所示,已知射线 DM与直线AB交于点A,线段EC与直线AB交于点C,AB∥DE.
(1)当∠MAC=100°,∠BCE=120°时,把EC绕点E旋转多大角度(所求角度小于180°)时,可判定MD∥EC?请你设计出两种方案,并画出草图;
(2)若将EC绕点E逆时针旋转60°时,点C与点A恰好重合,请画出草图,并在图中找出同位角、内错角各两对(先用数字标出角,再回答).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,P是直线l外一点,点A、B、C在l上,且PB⊥l,下列说法:①PA、PB、PC这3条线段中,PB最短;②点P到直线l的距离是线段PB的长;③线段AB的长是点A到PB的距离;④线段PA的长 是点P到直线l的距离.其中正确的是( )

A.①②③
B.①②④
C.①③④
D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a∥b,那么∠α的度数是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线y=
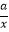 (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.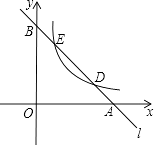
(1)若点D的坐标为(4,1),点E的坐标为(1,4):
①分别求出直线l与双曲线的解析式;
②若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形ABC中,AC=4 cm,BC=3 cm,将三角形ABC沿AB方向向右平移得到三角形DEF,若AE=8 cm,DB=2 cm.
(1)求三角形ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.

相关试题

