【题目】人教版八年级下册第19章《一次函数》中“思考”:这两个函数的图象形状都是直线,并且倾斜程度相同,函数![]() 的图象经过原点,函数
的图象经过原点,函数![]() 的图象经与y轴交于点(0,5),即它可以看作直线
的图象经与y轴交于点(0,5),即它可以看作直线![]() 向上平移5个单位长度而得到。比较一次函数解析式
向上平移5个单位长度而得到。比较一次函数解析式![]()
![]() 与正比例函数解析式
与正比例函数解析式![]() ,容易得出:一次函数
,容易得出:一次函数![]()
![]() 的图象可由直线
的图象可由直线![]() 通过向上(或向下)平移
通过向上(或向下)平移![]() 个单位得到(当b>0时,向上平移,当b<0时,向下平移)。
个单位得到(当b>0时,向上平移,当b<0时,向下平移)。
(结论应用)一次函数![]() 的图象可以看作正比例函数 的图象向 平移 个单位长度得到;
的图象可以看作正比例函数 的图象向 平移 个单位长度得到;
(类比思考)如果将直线![]() 的图象向右平移5个单位长度,那么得到的直线的函数解析式是怎样的呢?我们可以这样思考:在直线
的图象向右平移5个单位长度,那么得到的直线的函数解析式是怎样的呢?我们可以这样思考:在直线![]() 上任意取两点A(0,0)和B(1,
上任意取两点A(0,0)和B(1,![]() ),将点A(0,0)和B(1,
),将点A(0,0)和B(1,![]() )向右平移5个单位得到点C(5,0)和D(6,
)向右平移5个单位得到点C(5,0)和D(6,![]() ),连接CD,则直线CD就是直线AB向右平移5个单位长度后得到的直线,设直线CD的解析式为:
),连接CD,则直线CD就是直线AB向右平移5个单位长度后得到的直线,设直线CD的解析式为:![]() ,将C(5,0)和D(6,
,将C(5,0)和D(6,![]() )代入得到:
)代入得到:![]() 解得
解得![]() ,所以直线CD的解析式为:
,所以直线CD的解析式为:![]() ;①将直线
;①将直线![]() 向左平移5个单位长度,则平移后得到的直线解析式为 .②若先将直线
向左平移5个单位长度,则平移后得到的直线解析式为 .②若先将直线![]() 向左平移4个单位长度后,再向上平移5个单位长度,得到直线
向左平移4个单位长度后,再向上平移5个单位长度,得到直线![]() ,则直线
,则直线![]() 的解析式为: .
的解析式为: .
(拓展应用)已知直线![]() :
:![]() 与直线关于x轴对称,求直线的解析式.
与直线关于x轴对称,求直线的解析式.
参考答案:
【答案】【结论应用】y=x,下,3;
【类比思考】①y=-6x-30;②y=-6x-19;
【拓展应用】y=-2x-3.
【解析】
【结论应用】
根据题目材料中给出的结论即可求解;
【类比思考】
①在直线y=-6x上任意取两点A(0,0)和B(1,-6),将点A和B向左平移5个单位得到点C、D,根据点的平移规律得到点C、D的坐标.设直线CD的解析式为:y=kx+b(k≠0),利用待定系数法即可求出直线CD的解析式;
②在直线y=-6x上任意取两点A(0,0)和B(1,-6),将点A和B向左平移4个单位长度,再向上平移5个单位长度得到点C、D,根据点的平移规律得到点C、D的坐标.设直线CD的解析式为:y=kx+b(k≠0),利用待定系数法即可求出直线CD的解析式;
【拓展应用】
在直线![]() :y=2x+3上任意取两点A(0,3)和B(1,5),作点A和B关于x轴的对称点C、D,根据关于x轴对称的点的规律得到C、D的坐标.设直线CD的解析式为:y=kx+b(k≠0),利用待定系数法即可求出直线CD的解析式.
:y=2x+3上任意取两点A(0,3)和B(1,5),作点A和B关于x轴的对称点C、D,根据关于x轴对称的点的规律得到C、D的坐标.设直线CD的解析式为:y=kx+b(k≠0),利用待定系数法即可求出直线CD的解析式.
解:【结论应用】一次函数y=x-3的图象可以看作正比例函数y=x的图象向下平移3个单位长度而得到.
故答案为y=x,下,3;
【类比思考】①在直线y=-6x上任意取两点A(0,0)和B(1,-6),
将点A(0,0)和B(1,-6)向左平移5个单位得到点C(-5,0)和D(-4,-6),连接CD,则直线CD就是直线AB向左平移5个单位长度后得到的直线,设直线CD的解析式为:y=kx+b(k≠0),
将C(-5,0)和D(-4,-6)代入得到:
![]() ,
,
解得
![]() ,
,
所以直线CD的解析式为:y=-6x-30.
故答案为y=-6x-30;
②在直线y=-6x上任意取两点A(0,0)和B(1,-6),
将点A(0,0)和B(1,-6)向左平移4个单位长度,再向上平移5个单位长度得到点C(-4,5)和D(-3,-1),连接CD,则直线CD就是直线AB向左平移4个单位长度,再向上平移5个单位长度后得到的直线,
设直线CD的解析式为:y=kx+b(k≠0),
将C(-4,5)和D(-3,-1)代入得到:
![]()
解得![]()
所以直线![]() 的解析式为:y=-6x-19.
的解析式为:y=-6x-19.
故答案为y=-6x-19;
【拓展应用】在直线![]() :y=2x+3上任意取两点A(0,3)和B(1,5),
:y=2x+3上任意取两点A(0,3)和B(1,5),
则点A和B关于x轴的对称点分别为C(0,-3)或D(1,-5),连接CD,则直线CD就是直线AB关于x轴对称的直线,
设直线CD的解析式为:y=kx+b(k≠0),
将C(0,-3)或D(1,-5)代入得到:
![]()
解得
![]()
所以直线![]() 关于x轴对称的直线的解析式为y=-2x-3.
关于x轴对称的直线的解析式为y=-2x-3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+2019x+m=0与x2+mx+2019=0有且只有一个公共根,m的值为( )
A. 2019B. -2019C. 2020D. -2020
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止),此时的俯角为30°.为了便于观察,飞机继续向前飞行了800m到达B点,此时测得点F的俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A,B,C在同一直线上),竖直高度CF约为多少米?(结果保留整数.参考数据:
 ≈1.7)
≈1.7)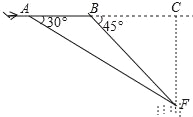
-
科目: 来源: 题型:
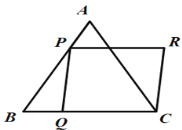
查看答案和解析>>【题目】如图,等边△ABC边长为4,点P,Q分别是AB,BC边上的动点,且AP =BQ= x,作□PQCR,则用含x的代数式表示□PQCR的面积为______;当PC∥AR时, x =____.
-
科目: 来源: 题型:
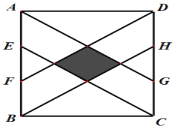
查看答案和解析>>【题目】如图,矩形ABCD的面积为2016,E、F、G、H分别是边AB,CD的三等分点,则图中阴影四边形的面积为___;若AB·BC=2016,AD:AB=8:9,则阴影四边形的周长为___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图5×5方格中,小正方形边长为1个单位长度,每个小正方形的顶点叫做格点.请按下列要求画出一个符合题意的四边形,且顶点在格点上,并写出所画图形的周长.

(1)在图1中画:是中心对称图形,但不是轴对称图形,且面积为8;
(2)在图2中画:既是中心对称图形,又是轴对称图形,且各边长都是无理数,面积为10.
相关试题

