【题目】如图在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,且
,且![]() 、
、![]() 满足
满足![]()
![]()
![]() 点
点![]() 表示的数为________;点
表示的数为________;点![]() 表示的数为________.
表示的数为________.
![]() 若点
若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 点表示的数________.
点表示的数________.
![]() 若在原点
若在原点![]() 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点![]() 处以
处以![]() 个单位/秒的速度向左运动;同时另一小球乙从点
个单位/秒的速度向左运动;同时另一小球乙从点![]() 处以
处以![]() 个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为
个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为![]() (秒),请分别表示出甲、乙两小球到原点的距离(用含
(秒),请分别表示出甲、乙两小球到原点的距离(用含![]() 的代数式表示).
的代数式表示).
参考答案:
【答案】(1)-5,7;(2)4或13;(3)当0≤t≤3.5时,小球到原点的距离为7-2t,当t>3.5时小球到原点的距离为2t-7.
【解析】
(1)根据非负数的性质列方程求出a、b的值,从而得解;
(2)根据两点间距离的表示列出绝对值方程,然后求解即可;
(3)甲小球根据数轴上的数向左减表示即可,乙小球分向左与向右移动两个部分分别列式表示即可.
解:(1)由题意得,a+5=0,b-7=0,
解得a=-5,b=7,
所以,点A表示-5,点B表示7;
(2)设点C表示x,由题意得,|-5-x|=3|7-x|,
所以,5+x=3(7-x)或5+x=-3(7-x),
解得x=4,或x=13,
所以,点C表示的数为4或13;
(3)甲:∵小球甲从点A处以1个单位/秒的速度向左运动,
∴甲到原点的距离为|-5-t|=5+t,
∵小球乙从点B处以2个单位/秒的速度也向左运动,
∴乙到达原点的时间为7÷2=3.5,
∴当0≤t≤3.5时,小球到原点的距离为7-2t,
当t>3.5时小球到原点的距离为2t-7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,BE平分∠ABC,CF平分∠BCD,BE、CF交于点G.若使EF=
 AD,那么平行四边形ABCD应满足的条件是( )
AD,那么平行四边形ABCD应满足的条件是( )
A.∠ABC=60°
B.AB:BC=1:4
C.AB:BC=5:2
D.AB:BC=5:8 -
科目: 来源: 题型:
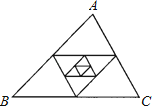
查看答案和解析>>【题目】 如图,△ABC的周长是32,以它的三边中点为顶点组成第2个三角形,再以第2个三角形的三边中点为顶点组成的第3个三角形,…,则第n个三角形的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,剪两张对边平行且宽度相等的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )

A. ∠ABC=∠ADC,∠BAD=∠BCD B. AB=BC
C. AB=CD,AD=BC D. ∠DAB+∠BCD=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=3cm,∠BAC=60°,那么△ABC能被半径至少为 cm的圆形纸片所覆盖.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形纸片ABCD中,
 ,
, ,将纸片折叠,使C,D落在AB边上的
,将纸片折叠,使C,D落在AB边上的 ,
, 处,折痕为MN,则
处,折痕为MN,则 ______度.
______度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)计算: 9 + ( π 2010 ) 0 2 cos 45 ° .
(2)先化简,再求值: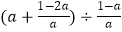 ,其中a=1﹣
,其中a=1﹣ 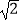 .
.
相关试题

