【题目】计算:
(1)计算: 9 + ( π 2010 ) 0 2 cos 45 ° .
(2)先化简,再求值: ![]() ,其中a=1﹣
,其中a=1﹣ ![]() .
.
参考答案:
【答案】
(1)
解: ![]() +
+ ![]()
=3+1﹣ ![]()
=3
(2)
解: 原式= ![]()
=1﹣a
当a=1﹣ ![]() 时,原式=1﹣1+
时,原式=1﹣1+ ![]() =
= ![]()
【解析】(1)根据平方根、0指数幂、特殊角的三角函数值的相关知识解答;(2)先将括号内的部分通分,再将除法转化为乘法进行化简,然后代入求值.
【考点精析】掌握零指数幂法则和特殊角的三角函数值是解答本题的根本,需要知道零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在数轴上
 点表示数
点表示数 ,
, 点表示数
点表示数 ,且
,且 、
、 满足
满足

 点
点 表示的数为________;点
表示的数为________;点 表示的数为________.
表示的数为________. 若点
若点 与点
与点 之间的距离表示为
之间的距离表示为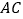 ,点
,点 与点
与点 之间的距离表示为
之间的距离表示为 ,请在数轴上找一点
,请在数轴上找一点 ,使
,使 ,则
,则 点表示的数________.
点表示的数________. 若在原点
若在原点 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点 处以
处以 个单位/秒的速度向左运动;同时另一小球乙从点
个单位/秒的速度向左运动;同时另一小球乙从点 处以
处以 个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为
个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为 (秒),请分别表示出甲、乙两小球到原点的距离(用含
(秒),请分别表示出甲、乙两小球到原点的距离(用含 的代数式表示).
的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=3cm,∠BAC=60°,那么△ABC能被半径至少为 cm的圆形纸片所覆盖.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形纸片ABCD中,
 ,
, ,将纸片折叠,使C,D落在AB边上的
,将纸片折叠,使C,D落在AB边上的 ,
, 处,折痕为MN,则
处,折痕为MN,则 ______度.
______度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形……,如此操作下去,那么,第6个三角形的直角顶点坐标为( )

A. (﹣
 ,
, ) B. (﹣
) B. (﹣ ,
, ) C. (﹣
) C. (﹣ ,
, ) D. (﹣
) D. (﹣ ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在由边长为1的小正方形组成的网格中,三角形ABC的顶点均落在格点上.

(1)将△ABC绕点O顺时针旋转90°后,得到△A1B1C1 . 在网格中画出△A1B1C1;
(2)求线段OA在旋转过程中扫过的图形面积;(结果保留π)
(3)求∠BCC1的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,
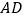 平分
平分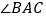 ,
,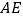 ⊥
⊥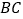 ,
,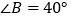 ,
,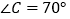 .
.【1】求
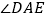 的度数
的度数【2】如图②,若把“
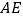 ⊥
⊥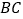 ”变成“点F在DA的延长线上,
”变成“点F在DA的延长线上,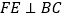 ”,其它条件不变,求
”,其它条件不变,求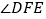 的度数;
的度数;【3】如图③,若把“
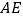 ⊥
⊥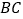 ”变成“
”变成“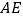 平分
平分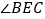 ”,其它条件不变,
”,其它条件不变,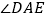 的大小是否变化,并请说明理由.(此题9分)
的大小是否变化,并请说明理由.(此题9分)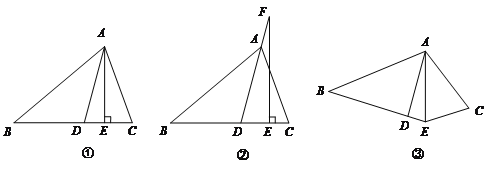
相关试题

