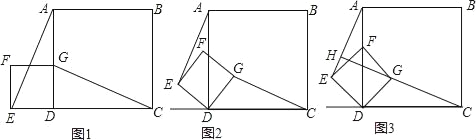
【题目】(1)如图1,正方形ABCD和正方形DEFG,G在AD边上,E在CD的延长线上.求证:AE=CG,AE⊥CG;
(2)如图2,若将图1中的正方形DEFG绕点D顺时针旋转角度θ(0°<θ<90°),此时AE=CG还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,当正方形DEFG绕点D顺时针旋转45°时,延长CG交AE于点H,当AD=4,DG=![]() 时,求线段CH的长.
时,求线段CH的长.
参考答案:
【答案】(1)(2)见解析;(3)![]() .
.
【解析】试题分析:(1)先判断出△ADE≌△CDG,然后用互余判断出垂直;
(2)先判断出△ADE≌△CDG,然后用互余判断出垂直;
(3)先判断出△ADE≌△CDG,然后用互余判断出垂直,然后用勾股定理计算出CM,AM最后用相似即可.
试题解析:(1)在△ADE和△CDG中,
DE=DG,∠ADE=∠CDG,AD=CD,
∴△ADE≌△CDG,
∴AE=CG,∠AED=∠CGD,
∵∠DCG+∠CGD=90°,
∴∠DCG+∠AED=90°,
∴AE⊥CG.
(2)∵∠CDG+∠ADG=90°,∠ADE+∠ADG=90°,
∴∠CDG=∠ADE
在△ADE和△CDG中,
DE=DG,∠ADE=∠CDG,AD=CD,
∴△ADE≌△CDG,
∴AE=CG,∠AED=∠CGD,
∵∠DCG+∠CGD=90°,
∴∠DCG+∠AED=90°,
∴AE⊥CG.
(3)如图,
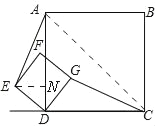
过点E作AD的垂线,垂足为N,连接AC,
在△ADE和△CDG中,
DE=DG,∠ADE=∠CDG,AD=CD,
∴△ADE≌△CDG,
∴∠EAD=∠DCM
∴tan∠DCM=![]() ,
,
∴DM=![]() CD=
CD=![]()
∴CM=![]() =
=![]() ,AM=AD﹣DM=
,AM=AD﹣DM=![]()
∵△CMD∽△AMH,
∴![]() ,
,
∴AH=![]() ,
,
∴CH=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+2bx+c(b、c为常数).
(Ⅰ)当b=1,c=﹣3时,求二次函数在﹣2≤x≤2上的最小值;
(Ⅱ)当c=3时,求二次函数在0≤x≤4上的最小值;
(Ⅲ)当c=4b2时,若在自变量x的值满足2b≤x≤2b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.
-
科目: 来源: 题型:
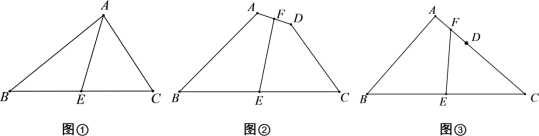
查看答案和解析>>【题目】(发现问题)爱好数学的小强在做作业时碰到这样的一道题目:如图①,在△ABC中,AB=8,AC=6,E为BC中点,求AE的取值范围.
(解决问题)
(1)小强经过多次的尝试与探索,终于得到解题思路:在图①中,作AB边上的中点F,连接EF,构造出△ABC的中位线EF,请你完成余下的求解过程.
(灵活运用)
(2)如图②,在四边形ABCD中,AB=8,CD=6,E、F分别为BC、AD中点,求EF的取值范围.
(3)变式:把图②中的A、D、C变成在一直线上时,如图③,其它条件不变,则EF的取值范围为 .
(迁移拓展)
(4)如图④,在△ABC中,∠A=60°,AB=4,E为BC边的中点,F是AC边上一点且EF正好平分△ABC的周长,则EF= .

-
科目: 来源: 题型:
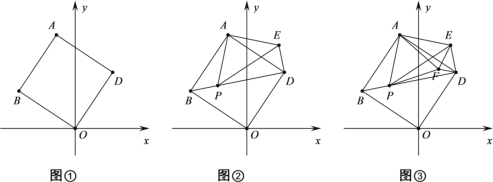
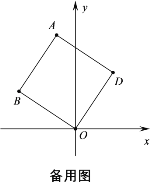
查看答案和解析>>【题目】如图①,将正方形ABOD放在平面直角坐标系中,O是坐标原点,点D的坐标为(2,3),
(1)点B的坐标为 ;
(2)若点P为对角线BD上的动点,作等腰直角三角形APE,使∠PAE=90°,如图②,连接DE,则BP与DE的关系(位置与数量关系)是 ,并说明理由;
(3)在(2)的条件下,再作等边三角形APF,连接EF、FD,如图③,在 P点运动过程中当EF取最小值时,此时∠DFE= °;
(4)在(1)的条件下,点 M在 x 轴上,在平面内是否存在点N,使以 B、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=
 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.(1)求函数y=kx+b和y=
 的表达式;
的表达式;(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据:
 ,结果保留整数.)
,结果保留整数.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,… 组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒
 个单位长度,则第2019秒时,点P的坐标是________________
个单位长度,则第2019秒时,点P的坐标是________________
相关试题

